Why We Use Z-Transform Instead of Laplace?
Follow articleHow do you feel about this article? Help us to provide better content for you.
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
What do you think of this article?
As technology continues advancing, the need for efficient signal processing has become increasingly important. Transform methods provide an effective way to analyze signals and systems in different domains. Two of the most powerful and widely used transform methods are Laplace transform and z-transform. However, while they may seem similar, important differences between these two methods make them better suited for different applications.
In this article, we'll explore why we use z-transform instead of Laplace transform in certain signal processing applications. Then, we'll take a closer look at the strengths and limitations of each method and discuss why z-transform is particularly useful for analyzing discrete-time signals and systems. You'll have a deeper understanding of these powerful transform methods and be better equipped to choose the right tool for your signal processing needs.
Difference Between Laplace and Z-Transform
Laplace transform and z-transform are two of the most important mathematical tools used in signal processing. These transform methods provide an efficient way to analyze signals and systems in different domains. However, while they may seem similar, important differences between the two make them better suited for different types of signals and systems.
Laplace transform is a method used to analyze continuous-time signals and systems. It is based on the complex plane, with the Laplace transform of a signal representing its complex frequency response. The Laplace transform is usually used in solving differential equations, making it a powerful tool in many applications.
On the other hand, z-transform is used for analyzing discrete-time signals and systems. Unlike Laplace transform, z-transform is based on the unit circle in the complex plane, with the z-transform of a signal representing its complex frequency response in the z-domain. Z-transform is also used to solve difference equations, which makes it particularly useful in digital signal processing.
One of the key differences between the Laplace transform and z-transform is the type of signals they are best suited for. Laplace transform is most effective in analyzing continuous-time signals, while z-transform is better suited for discrete-time signals. Laplace transform is also more powerful in solving differential equations, while the z-transform is more efficient in solving differential equations.
Another important difference between the two transforms is the type of analysis they can perform. For example, Laplace transform with MATLAB is commonly used in the stability analysis of continuous-time systems, while z-transform is more useful in stability analysis of discrete-time systems. In addition, Z-transform is also used in the analysis of finite-duration signals, which is not possible using the Laplace transform.
In addition, z-transform has a direct relationship with discrete Fourier transform (DFT), widely used in signal processing applications. The relationship between z-transform and DFT allows for the efficient implementation of digital filters, making z-transform a popular tool in digital signal processing.
Applications of Laplace and Z-Transform
Laplace and z-transforms are two powerful mathematical tools with a wide range of applications in signal processing. The following sections describe some of the applications of these transforms in different areas of engineering and science.
Applications of Laplace Transform
- Laplace transform is widely used to analyze and design control systems, particularly in the time domain. It provides a way to convert differential equations into algebraic ones, which can be easily solved using standard techniques.
- Laplace transform is commonly used to analyze electrical circuits. Applying Laplace transform to the circuit equations makes it possible to determine the circuit's behaviour under different conditions, such as steady-state or transient response.
- Laplace transform analyzes communication systems like radio, TV, and telephone systems. Converting signals into the Laplace domain makes it possible to analyze the system's frequency response, which is essential in designing filters and amplifiers.
- Laplace transform is used in many signal-processing applications, such as speech, image, and biomedical signal processing. It provides a way to analyze signals in the frequency domain, which is useful for filtering, compression, and enhancement.
Applications of Z-Transform
- Z-transform is used extensively in digital signal processing, particularly in analyzing and designing digital filters. By converting signals into the z-domain, it is possible to analyze the filter's frequency response and design it to meet specific requirements.
- Z-transform is used to analyze and design digital control systems, particularly in the design of discrete-time controllers. It provides a way to convert differences into algebraic equations, which can be easily solved using standard techniques.
- Z-transform is used in image processing applications, such as image compression and filtering. It provides a way to analyze images in the frequency domain, which is useful for filtering, enhancement, and compression.
- Z-transform analyzes digital communication systems, such as digital modems and codecs. By converting signals into the z-domain, it is possible to analyze the system's frequency response and design it to meet specific requirements.
Why We Use Z-Transform Instead of Laplace?
While Laplace and z-transform in MATLAB are powerful mathematical tools for signal analysis and processing, there are specific scenarios where the z-transform is preferred over the Laplace transform. The following sections describe some of the reasons why we use z-transform instead of Laplace.
- Discrete-Time Systems: One of the primary reasons why the z-transform is used instead of the Laplace transform is when dealing with discrete-time systems. The z-transform handles discrete-time signals, whereas the Laplace transform best suits continuous-time signals. Therefore, when working with digital signals, such as those found in digital signal processing and control systems, the z-transform is the preferred method for analyzing these signals.
- Finite Length Signals: The z-transform is better suited for analyzing finite length signals than the Laplace transform. The z-transform is a finite-length transform, which means it can handle signals with a finite duration. In contrast, the Laplace transform is an infinite-length transform, which means it is better suited for signals with an infinite duration. Therefore, when dealing with signals with a finite duration, such as those found in image processing and audio signal processing, the z-transform is often preferred over the Laplace transform.
- Stability Analysis: The z-transform is better suited for analyzing the stability of discrete-time systems than the Laplace transform. It is because the z-transform provides a way to analyze the poles and zeros of the transfer function of a system, which are important indicators of stability. In contrast, the Laplace transform is better suited for analyzing the behaviour of continuous-time systems, where stability analysis is based on the poles' location in the complex plane's left half-plane.
- Sampling Theory: The z-transform is closely related to the sampling theory, the basis for digital signal processing. The z-transform can be used to derive the discrete Fourier transform, an important tool in digital signal processing. Therefore, when working with digital signals, the z-transform is often preferred over the Laplace transform, as it provides a more direct connection to the underlying digital signal processing theory.
Conclusion
Signal processing is a constantly evolving field that relies heavily on transform methods for analyzing and processing signals. Laplace transform and z-transform are two of the most commonly used methods, each with its strengths and limitations. While Laplace transform is best suited for analyzing continuous-time signals and systems, z-transform is preferred for discrete-time signals and systems.
Its ability to analyze finite-duration signals and perform a stability analysis of discrete-time systems and its close relationship with DFT makes z-transform a powerful tool in signal processing applications. By understanding the differences between these two transforms, researchers and practitioners can choose the most appropriate tool for their specific application, leading to more accurate and efficient analysis and enabling them to make discoveries in this fascinating field.


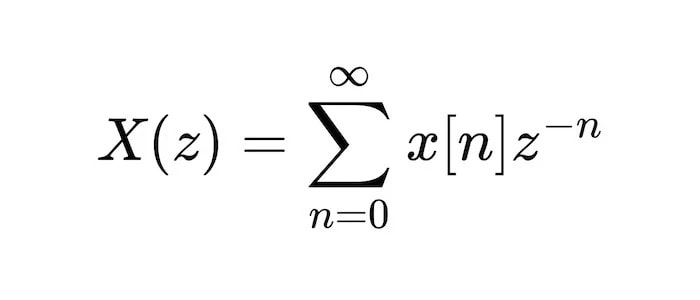
Comments