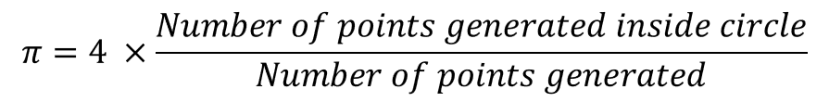How much faster can an algorithm run in FPGA fabric than in a processor?
Follow articleHow do you feel about this article? Help us to provide better content for you.
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
What do you think of this article?
Field Programmable Gate Array (FPGA) is an array of logic gates that are hardware-programmed to perform a user-specified task. FPGAs provide the advantage of incorporating parallelism which many calculations or instructions are carried out simultaneously. This significantly enhances the computational speed compared to processor-based platforms. Thanks to high-speed embedded resources such as DSP slices and fast memories, FPGAs are now also utilized for algorithm acceleration.
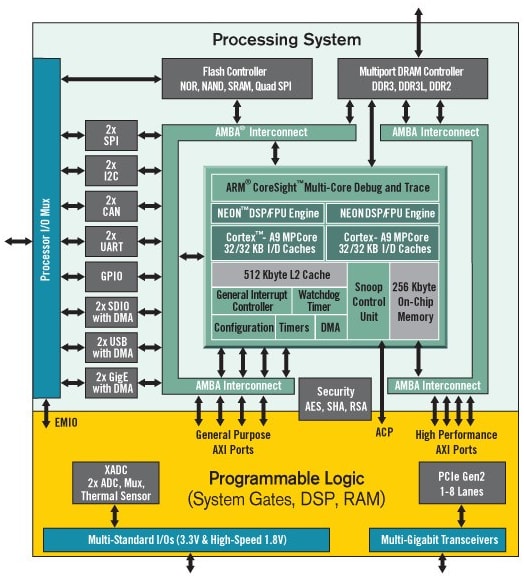
This project compares the speed at which a Pi Estimation algorithm runs in FPGA hardware to how fast the same algorithm runs on a processor. A Monte Carlo Pi Estimation algorithm runs on both processor and FPGA fabric of Digilent Cora Z7 Zynq-7000 Single Core and Dual Core Options for ARM/FPGA SoC Development. Xilinx Zynq-7000 architecture tightly integrates a single or dual core 667MHz ARM Cortex-A9 processor with a Xilinx 7-series FPGA.
Zynq APSoC Architecture
Cora Z7 product variants are referred to as the Cora Z7-10 (184-0484) and Cora Z7-07S (184-0456) respectively. The only difference between the Cora Z7-10 and Cora Z7-07S is the capability of the Zynq part. The Cora Z7’s wide array of hardware interfaces, from a 1Gbps Ethernet PHY to analog-to-digital converters and general-purpose input/output pins, make it an ideal platform for the development of a vast variety of embedded applications.
| Product Variant | Cora Z7-10 | Cora Z7-07S |
| Zynq Part | XC7Z010-1CLG400C | XC7Z007S-1CLG400C |
| ARM Processor Cores | 2 | 1 |
| 1 MSPS On-chip ADC | Yes | Yes |
| Look-up Tables (LUTs) | 17,600 | 14,400 |
| Flip-Flops | 35,200 | 28,800 |
| DSP Slices | 80 | 66 |
| Block RAM | 270 KB | 225 KB |
| Clock Management Tiles | 2 | 2 |
Cora Z7 Zynq 7000 Platform
Estimating Pi using Monte Carlo Method
There are many websites explaining Pi Estimation through Monte Carlo Method. You can check out this website The rationale is to generate a large number of random points and see how many fall in the circle enclosed by the unit square. The area of a square is 1 while the area of circle is pi / 4 since the radius is 0.5. With a large number of random points (x,y),
To implement the algorithm, you simply generate random point (x, y) and then check if distance of the point from the origin (x,y) is less than or equal to 1 (x2 + y2 <= 1). If yes, you increment the number of points that appears inside the circle.
Run the algorithm on ARM Processor and in Linux
The tutorial teaches you how to boot Linux on Cora Z7 ARM Processor. Then you can use Go programming language to estimate the Pi through the Monte Carlo Method. What you need are Ubuntu 16.04.3, Xilinx Viavdo 2017.4, Petalinux, Golang. Golang can be installed through apt-get, but the other tools need to be downloaded through Xilinx's website. You need to use Petalinux to boot into Linux.
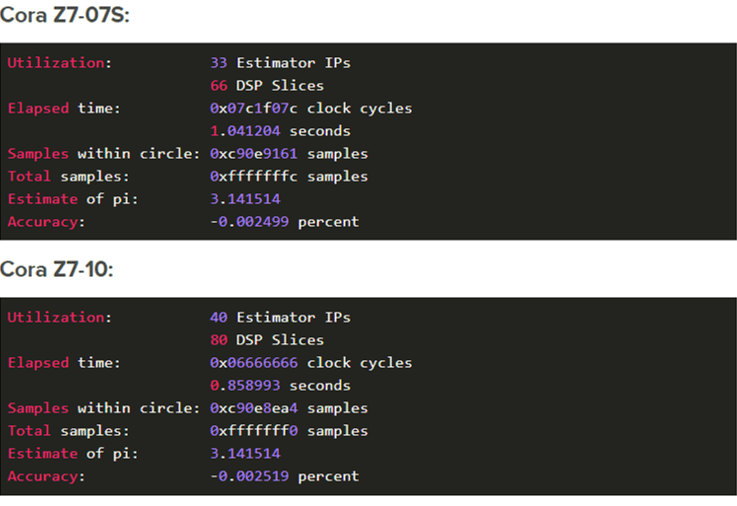
The table below shows how long each of the Cora Z7 variants took to process 100,000 Monte Carlo samples.
Run the algorithm in the FPGA fabric
The tutorial shows you how to build the algorithm in FPGA logic. The FPGA fabric contains elements called digital signal processing (DSP) slices. In the case of running the Monte Carlo method, you need to do two multiplication operations (x*x and y*y). As long as the result of each multiplication operation is less than 48 bits wide, you only need to use two of the Cora's DSP slices per instance of the code running the Monte Carlo simulation. Random samples are created by using a linear feedback shift register (LFSR), with a seed value provided by the controller. The clock of the entire system is 125MHz. Chose to run as many samples as you could fit in a 32-bit integer
See the results printed by each Cora variant pasted below:
FPGA Vs Processor
Where the slower of the two Cora Z7 variants was able to process a full 32-bit integer's worth of samples in about a second, the faster of the two only managed 100,000,000 samples in 1.8 seconds in Linux. In other words, the hardware-accelerated version of the algorithm was 77 times faster. The FPGA design can process 9 of the Monte Carlo samples per clock cycle (one clock cycle per 8 nanoseconds).