Blockchain Primer - Part 1
Follow articleHow do you feel about this article? Help us to provide better content for you.
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
What do you think of this article?
If you were to believe the hype, you might get the impression that blockchain is poised to end disease, poverty and hunger while ushering in a golden age of world peace. While it may not be the panacea that some marketing departments would have you believe, it is a dependable tool that offers a credible solution for many applications.
To decide which applications suit blockchain (and which don’t) it helps to have a handle on the theory behind blockchain and its implementation. In this article, I will attempt to provide an ‘executive summary’ of what you need to know in order to make your own decisions about this exciting technology.
Genesis
Contrary to popular opinion, blockchain did not spring, fully formed and armoured, from the mind of Satoshi Nakamoto like some modern, software-based Athena.
The original concepts can be traced back to a 1991 paper by Stuart Haber and W. Scott Stornetta titled 'How to Time-Stamp a Digital Document' where they wrestled with the problem of how to timestamp digital data so that it would become unfeasible to backdate (or forward date) the data once stamped.
In the days when pretty much anything digital could easily be spoofed, this was a pithy conundrum for engineers who wanted to use networking technology to enable everything from collaborative, remote working to digital transactions.
The security concepts developed by Haber and Stornetta were built upon by Satoshi Nakamoto (whoever he, she or they turn out to be) in the creation of Bitcoin.
Genesis Block
There are any number of loosely related definitions out there for what constitutes a blockchain, but the definition I will use is this:
“A continuously growing list of records, called blocks, which are linked and secured using cryptography.”
The way that the records are linked and secured is using a technique called hashing. We will get into exactly what this entails a little later, but for now, you can think of a hash algorithm as something that takes a ‘fingerprint’ of a block of data. Like a fingerprint, a hash is (close to) unique.
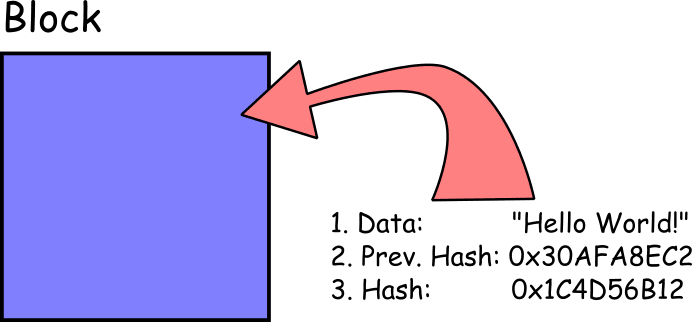
A minimally viable block will contain at least 3 things:
The ‘data’ can be pretty much anything you like, though it will typically be a small set of elements: the kinds of things that would historically have been entered on a line in a paper-and-ink ledger. This could include records such as financial transaction information, the GPS coordinates for the location of a shipping container or the heart-rate and blood pressure of a hospital patient. It can also be an empty or null value to show that no data was recorded at a particular time.
The 'hash' is the hash value of the block contents – in this case, it will be the hash value of the data and the previous hash.
The ‘previous hash’ is what allows us to cryptographically link blocks together, starting from the first block, known as the ‘Genesis Block’. The Genesis Block is a special case and will not have a previous hash as it is the first block in the chain:
This cryptographic link to the previous block gives the chain an important property. If the data in block 1, for example, is tampered with in any way the hash value for that block will change. The new hash value for block 1 will no longer match the value of ‘previous hash’ stored in block 2 and can be easily detected and flagged so that the change can be rejected.
It is the chaining together of the blocks in this way that ensures the integrity of the stored data.
The two questions that might spring to mind at this point are “..but couldn’t you just fake the hash value in some way?” or “..couldn’t you just run through the chain and change all the ‘previous hash’ values to hide the tampering?”
In order to understand why neither of these things is computationally feasible, we need to know a little about the nature of hash algorithms.
Requirements For A Hash Algorithm
There are five requirements for a hash algorithm if it is going to be effective in a blockchain:
- Deterministic – The same data input to the algorithm will always produce the same hash value result.
- One Way – The original data cannot be reconstructed from the hash.
- Avalanche Effect – Even the smallest possible change to the original data will result in a completely different hash.
- Fast Computation – Applying the algorithm to a block of data requires a minimal number of processor cycles to produce the result allowing the calculations to be done quickly.
- Collision Tolerant – When data sets outnumber the total combinations available to the algorithm then a re-used hash will occur: a collision. This should be an extremely rare occurrence and the algorithm cannot permit forced collisions which would allow data faking.
A hash algorithm that adheres to these constraints will take input data of any length – from the letter ‘a’ to the contents of the Encyclopaedia Britannica in its entirety – and quickly return a fixed length output which is a representative fingerprint of the data. Ideally, a secure hash is indistinguishable from a random mapping and even the smallest change in the data will result in a wholly different hash. You can get an empirical feel for how this works using this online SHA256 Hash Generator.
Rainbow Tables: Although the hash function is one way, meaning the original data can’t be reconstructed from the hash output, the deterministic nature of algorithms like (Secure Hashing Algorithm) SHA256 means that if you already know (or can narrow down) the input data, it is relatively quick to confirm that you have the right data by checking against a list of hash outputs for known inputs. The last line of defence against hackers compromising passwords is to store them in a hashed form. However, widely available rainbow tables that link common passwords with their hash output, allow hackers to easily extract weak and common passwords by simply running through the tables until they find the hash value. A defence against this is ‘salting’ the hash by adding other character sequences to the passwords before hashing, to invalidate the most common rainbow tables."
Collision Resistance
Collision resistance is the real measure for the strength of a hash algorithm. It is a measure of how unlikely it is that two different inputs will produce the same resultant hash.
By the pigeonhole principle, we would guess that if we have a number of n possible hash values then if we have one more than n (i.e. n + 1) inputs, then we are likely to get a shared hash value. For SHA256 that would equate to 2256 (or 6436) possible hash values.
Unfortunately, the universe is a little more perverse than simple intuition. The laws of probability, specifically what is known as the Birthday Paradox (aka the Birthday Problem) tell us that the true probability of a collision for large numbers is the square root of n. That would mean we can ‘only’ calculate 2128 hash values before a collision is likely.
To put that into some perspective, if we have a computer calculating 232 hashes per second it should take 296 seconds before a collision. Which is about 2.5 x 1021 years: a fair bit more than the current estimate for the age of the universe (1.4 x 1010 years) and certainly way more than the warranty period of a computer that’s running flat out 24/7.
There is more to the mathematics, which some folks seek to exploit in mounting birthday attacks and similar collision attacks but for our purposes, it is enough to know that, so far, SHA256 has resisted these types of attacks.
Summary
We have looked at the basic theory of how a blockchain connects data blocks together to secure data using hash functions. In part 2 we will look at mining, how operational blockchains are distributed across P2P networks and how they deal with errors and/or attacks.