LoRa Location Tracker Part 2: RSSI
Follow articleHow do you feel about this article? Help us to provide better content for you.
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
What do you think of this article?
LoRa Location Tracker Part 2: RSSI
Starting from where I stopped in Part 1, about how to use LoRa to be the ideal location tracker and why I chose LoRa. Now I can first measure the RSSI value per meter and get the conversion equation between the RSSI value and the distance. After getting this equation, I can easily calculate the target position by using my LoRa module.
What is RSSI?
RSSI (Received Signal Strength Indicator) is an estimated measurement of the power level received by an RF client device from an access point or router. The RSSI value will be affected by different reasons, such as different venues, modules, and antennas.
Through the RSSI value, we can convert the value to a distance.
In my project, I use 3 RSSI values that match the triangle to calculate the target position. Therefore, the conversion accuracy of RSSI and distance is very important to me. Then I tried to measure the RSSI value of the relative distance and plot a graph to get the conversion equation.
Process
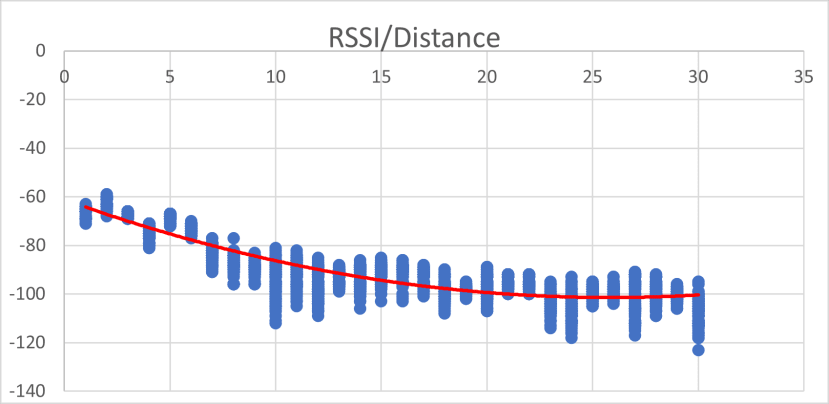
First, I measure the RSSI value for every meter, plot an RSSI Distance graph.
I found that it is an exponential curve, so I must take the log of the distance to get the linear equation.
In the above graph, I have y = -32.324x - 55.465.
It means,
RSSI = -32.324log(distance) - 55.465
RSSI = -20αlog(d)+20αlog(d0)
RSSI = Received Signal Strength Indication
α = Path Loss Exponent (Constant)
d0 = Reference distance
d = Distance between the Sender and Receiver
Now, I got the conversion equation between RSSI and distance. Through this equation, I can enter the program and get the distance between the target and the receiver. It makes RSSI meaningful and easy to read.
Accuracy:
In addition to the RSSI equation, I also want to know the RSSI data I recorded to measure the accuracy of my equipment. In each meter, I measure multiple RSSI values. Though these data, I tried to calculate the accuracy of each meter and summarize the performance of my equipment.
Process
In Excel, I need to find out the normal distribution of each meter,
=NORMDIST(x,mean,standard_dev,cumulative)First Quartile(Q1),
=QUARTILE(A1:A10,1)Third Quartile(Q3),
=QUARTILE(A1:A10,3)Interquartile Range (IQR),
=Q3-Q1Lower Boundary (LB),
= Q1-(1.5*IQR)Upper Boundary (UB)
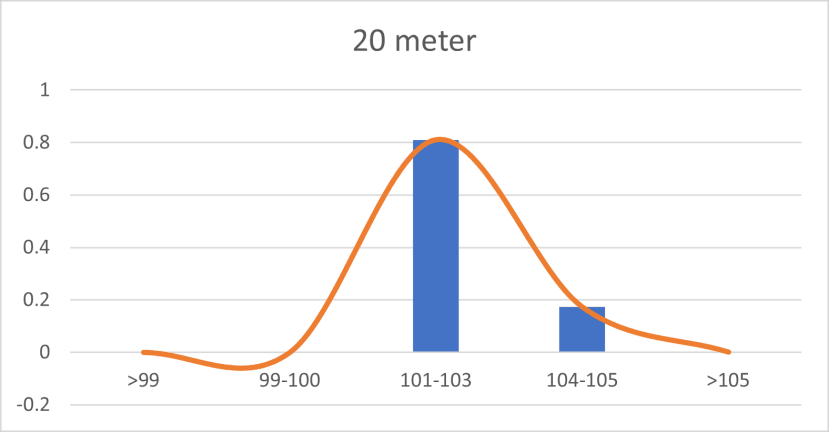
= Q3+(1.5*IQR)Finally, I can unify group boundaries and plot the graph.
The figure above shows that the accuracy of the 20m transmission distance is 80% accuracy between the RSSI between 101 and 103.
Further Development:
Summarizing all the data I got, I found that the positioning accuracy of my LoRa module can reach about 80%. This is good news for me. In Part 3, I will mainly focus on building a server and an application to monitor the target position.