Heroes of Tech: Claude Shannon
Follow articleHow do you feel about this article? Help us to provide better content for you.
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
What do you think of this article?
This article is the first in a short series that looks at the lives of people whose contributions are the ‘sine qua non’ of the modern world. We start with Claude Shannon, a man who has influenced nearly every aspect of the technology we interact with every day. Mathematician and electrical engineer Solomon W. Golomb once commented that Shannon’s effect on the digital age has been profound:
“It’s like saying how much influence the inventor of the alphabet has had on literature”
Bio
Claude Shannon Jr was born on April 30th 1916 in Petoskey, Michigan to a probate judge, Claude Elwood Shannon and high school principal, Mable (née Wolf). Young Claude was technically adept and loved to build things with his hands, a near-obsession that continued into old age.
In 1936, Shannon received a bachelor of science degree from the University of Michigan. He wasn't sure what to do next, but happened to see a card on the wall advertising a job at the Massachusetts Institute of Technology, working for Vannevar Bush, maintaining a new computer called the Differential Analyzer. Shannon applied for the job. The Differential Analyzer was an electrically driven, mechanical computer the size of a two-car garage that relied on gear ratios to represent numbers in the problems to be solved. It took a few days to set up an equation and several more to get a plotted graph as an output.
Digital Computing
Shannon recognised the glaring flaws in this way of doing things and pictured an entirely electrical computer where on/off states would represent numbers. He had learned Boolean algebra as an undergraduate and understood that any logical relationship can be put together from a combination of IF, TRUE/FALSE, AND, OR and NOT. Shannon physically built each of these logical ideas into electrical circuits, proving that an electronic digital computer could compute anything. Shannon published this idea in 1937, in what some have called the most important master’s thesis of the 20th century, forming the foundation of digital circuit design and hence digital computing.
Genetics
Bush recognised that Shannon had a near-universally applicable genius that could be channelled in any direction and insisted that the mathematics department accept Shannon for his doctoral work. He also saw that Shannon had a somewhat capricious focus and guided him towards using his talents in the field of genetics. After some initial work and then a summer fellowship with Barbara Burks at the Eugenics Record Office at Cold Spring Harbor, on Long Island, Shannon's PhD thesis was titled “Algebra for Theoretical Genetics.” Shannon used mathematics to study how different allele combinations propagated through several generations of breeding. His unique theorem in the paper was not independently rediscovered for another decade. It had to be rediscovered because the paper was never published in a journal: mercurial as he was, Shannon had already lost interest in the field and moved on.
Shannon went from a summer at Bell Labs’ Greenwich Village site to the Institute for Advanced Study at Princeton for a year of postdoctoral work under mathematician and physicist Hermann Weyl and then on to the U.S. Office of Scientific Research and Development. By 1941 he was back at Bell Labs and became involved in Project X.
Project X
This was a joint effort between Bell Labs and the Government Code and Cipher School at Bletchley Park with a scientific pedigree to rival the Manhattan Project. The Anglo-American team included both Shannon and Alan Turing, building a system known as SIGSALY - which wasn't an acronym but a random string of letters meant to confuse the Germans, should they ever become aware of it. The aim was to make sure that the advantage the allies had, after Turing had cracked the Enigma code, remained solely with the allies.
SIGSALY was the first digitally scrambled, wireless phone. As a side note, if you read no other link here, the SIGSALY link is tech-history geek heaven and well worth your time. It used an unbreakable Vernam cypher or “onetime pad” encryption key in the form of a vinyl LP record of random “white noise” which was added to the speaker's voice producing an indecipherable hiss. An identical vinyl record was used to subtract the noise on the other end.
After the war (in 1949) Shannon published what is arguably the foundational paper of modern cryptography, "Communication Theory of Secrecy Systems" where he discussed cryptography from the viewpoint of information theory; formally defining, mathematically, what perfect secrecy meant and proving that all theoretically unbreakable ciphers have the same requirements as the one-time pad.
Alan Turing
When Alan Turing visited Bell Labs’ New York offices in 1943, it was clear they enjoyed each other's company and they met daily in the lab cafeteria. Shannon told Turing he was working on a way of measuring information with a unit called the 'bit'. Shannon credited the term to another Bell Labs mathematician, John Tukey, but where Tukey’s bit was short for “binary digit, Shannon defined it as the amount of information needed to distinguish between two equally likely outcomes.
Magnum Opus
Shannon published “A Mathematical Theory of Communication” in a 1948 issue of the Bell System Technical Journal. Both this and the ‘Secrecy Systems’ paper of 1949, derive from a technical report, A Mathematical Theory of Cryptography, written by Shannon in 1945. The circulation list for this report includes Black, Nyquist, Bode, and Hartley.
That both papers should come from the same work might seem surprising but as Shannon is quoted as saying in David Kahn’s 1967 book The Codebreakers:
“The work on both the mathematical theory of communications and the cryptography
went forward concurrently from about 1941. I worked on both of them together
and I had some of the ideas while working on the other. I wouldn't say that one
came before the other--they were so close together you couldn't separate them.”
It’s interesting to note that this was another body of work in danger of never being published. Shannon had developed the theory out of pure curiosity and was ready to investigate other things. But when Bell Labs colleagues learned of this work, they couldn’t believe that Shannon had devised such important results and then sat on them. They organised what was essentially a scientific intervention to force Shannon to publish the theory. Once he did, he moved on.
Marvin Minsky reflected once that Shannon stopped working on information because he felt he had proven everything worth proving. Which was probably true. Robert Fano remembered that, with rare exceptions, whenever an information theorist approached Shannon with a current problem, Shannon was already aware of the problem and had already solved it. He just hadn’t gotten around to publishing it.
Later Work
Shannon began teaching at MIT in the spring of 1956 and that was the beginning of the end of his career as a publishing scientist. However, his eclectic contributions after this point were often still profound.
Shannon organized the first major academic conference on artificial intelligence at Dartmouth College, New Hampshire in 1956. This was a field that took his interest and earlier, in 1950, he had built an early illustration of AI in the form of a robotic mouse called Theseus that could navigate and then remember a path through a maze. The same year, he published a paper titled “Programming a Computer for Playing Chess” which formed the basis for the first chess game played by a computer, the MANIAC I, against a human in 1956 and most subsequent chess algorithms.
Shannon also worked with fellow mathematics professor Edward Thorp to build the first wearable computer, designed (and tested!) to beat the roulette tables in Vegas. Also in the realm of gambling, Shannon had a hand in the development of the Kelly criterion.
A Mathematical Theory of Communication
"A basic idea in information theory is that information can be treated very much
like a physical quantity, such as mass or energy."
Claude Shannon, 1985.
It is hard to think of anyone else since the Renaissance who has created a whole new scientific disciple out of the ether and influenced so many more.
In the early 1940’s information was viewed as a poorly defined substance; something almost akin to a fluid and no-one believed it was possible to send and receive error-free signals. Shannon’s 1948 paper was so ground breaking because it turned conventional wisdom on its head by clearly defining information and showing how it could be transmitted without error.
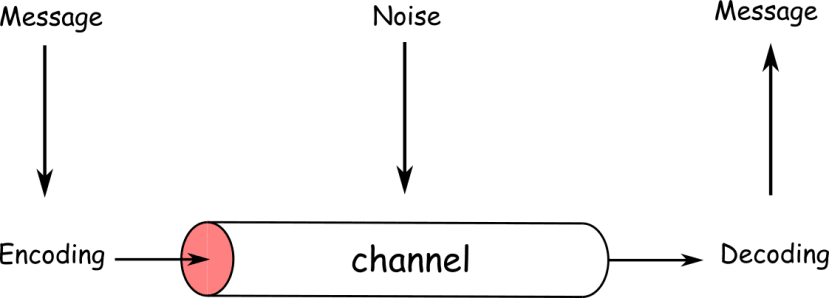
A standard communication channel
The key take-aways from his work were:
- For any communication channel there is a definite upper limit, the channel capacity (or Shannon Limit), to the amount of information that can be communicated through that channel.
- This limit shrinks as the amount of noise in the channel increases.
- The limit can be asymptotically approached by shrewd packing (i.e. encoding) of data.
Each of these ideas has profound implications.
Channel Capacity & The Noisy Channel Coding Theorem
The fundamental axiom of information theory is that given a channel with a particular bandwidth and noise characteristics, a definable speed limit for error-free data transmission exists. Measured in bits per second: this is the channel capacity or Shannon Limit.
C = Channel Capacity (bits/s)
B = Bandwidth (Hz)
S = Signal Power (W)
N = Noise Power(W)
Above this limit, it is mathematically impossible to get error-free communication, regardless of the sophistication of any error correction scheme you might use. Information will be lost.
However, on the flip side, below this limit, it is possible to transmit information without error. Shannon proved statistically that there was always a method of encoding information that would allow information to get up to the limit without any errors: regardless of the amount of noise or static, or how faint the signal.
The noisy channel coding theorem gave rise to the entire field of channel coding and error-correction coding, where deliberate redundancy is introduced into the digital signal representation to protect against degradation. The two main categories of ECC codes are block codes, that work on work on fixed-size blocks (packets) of data and convolutional codes that work on bitstreams of arbitrary length.
Entropy
Shannon also discussed ‘source coding’ or data compression. The objective of source coding is to remove redundancy in the signal to make the message smaller. He introduced a loss-less variable rate data compression scheme that became known as the Shannon-Fano code. Three years later Fano’s student, David Huffman, developed a more optimised code which is still widely used for data compression in JPEGS, MP3s and .ZIP files.
In his discussion, Shannon also demonstrated that information in a signal has an irreducible complexity, below which the signal cannot be compressed, and this is the amount of unexpected data the message contains.
When Shannon was looking for a term for this information content, John von Neumann of Princeton’s Institute for Advanced Study advised Shannon to use the word entropy. He told Shannon: Use “entropy” and you can never lose a debate, because no one really knows what “entropy” means! The name stuck.
In digital comms, a stream of unexpected bits is just random noise but Shannon showed that the more a transmission resembles random noise, the more information it can hold; so long as it is modulated to an appropriate carrier: a high entropy message needs a low entropy carrier.
Digitisation
Perhaps the most radical idea for engineers of the late 1940's was Shannon's proposal that the original form of the information was irrelevant. Text, sound, images, or video could all be encoded as 0’s and 1’s to a communication channel. Once digital, data could be regenerated and transmitted without error. This vision unified all of communication engineering: telegraphy, telephony, audio and data transmission could all be encoded in bits; the basis of the internet and most communication forms we use today.
Conclusion
It has been impossibly hard to par down the life of an intellectual and engineering colossus like Claude Shannon into a short article without it being the merest impression, leaving out so much of the colour and texture of the man himself. Hopefully, we have presented enough to spark your interest in further research, as he was also such an intriguing character, who was married twice, enjoyed Dixieland music, was known to his colleagues for being an accomplished juggler who would unicycle (while juggling) round the corridors of Bell Labs at night and loved to build ridiculous contraptions – perhaps epitomised by his ‘Ultimate Machine’.
It’s said that just about everyone who knew Shannon at all, liked him and he certainly tops my list of engineering heroes.





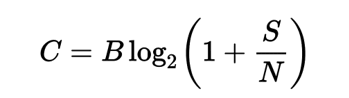
Comments