Die Räder zum Drehen bringen: Einen Dauermagnet-Gleichstrommotor auswählen
Artikel folgenWie finden Sie diesen Artikel? Helfen Sie uns, bessere Inhalte für Sie bereitzustellen.
Vielen Dank! Ihr Feedback ist eingegangen.
There was a problem submitting your feedback, please try again later.
Was denken Sie über diesen Artikel?

Mein letzter Beitrag Die Räder zum Drehen bringen: Dauermagnet-Gleichstrommotoren mit einem Mikrocontroller verbinden behandelte Schnittstellen-Hardware und die Verwendung von PWM zur Drehzahlregelung. Als Reaktion auf den Kommentar eines DesignSpark-Mitglieds möchte ich die grundlegenden Punkte behandeln, die zu beachten sind, wenn man den Dauermagnet-Gleichstrommotor für ein bestimmtes Projekt auswählt. Es folgt nun eine stark vereinfachte Darstellung des Entwicklungsprozesses, mit der die ungefähre Größenordnung der für den Entwurf benötigten Parameter ermittelt werden kann.
Wesentliche Merkmale
Zunächst sollten Sie sich das Diagramm „Drehmoment im Vergleich zur Drehzahl“ in meinem letzten Beitrag (und in Abb. 1 weiter unten) ansehen. Die ersten drei zu ermittelnden Motorparameter sind die Werte für Stillstandsdrehmoment, manchmal auch Anlaufdrehmoment genannt, Betriebsdrehmoment und Leerlaufdrehzahl. Nimmt man einen zweirädrigen mobilen Buggy-Roboter als Beispielprojekt, so muss man herausfinden, wie viel Drehmoment jedes Rad benötigt, um die Haftreibung zu überwinden und den Roboter in Bewegung zu setzen. Hat man genügend Daten zu Reibung zwischen Rad und Boden, Haftung und so weiter, so lässt sich alles, was man wissen muss, von Grund auf berechnen. Wenn Sie kein Ingenieur sind, der am nächsten NASA-Rover arbeitet, lohnt sich der Arbeits- und Zeitaufwand aber nicht. Es ist besser, zuerst den Buggy zu bauen und dann ein paar Experimente damit durchzuführen, wenn Motoren und Getriebe noch nicht montiert sind.
 Kraftmessung durchführen
Kraftmessung durchführen
Sie benötigen ein Instrument zur Kraftmessung: Eine einfache Federwaage, die für einen kleinen Roboter in Gramm oder für einen großen Roboter in Kilogramm kalibriert ist. Eine größere Genauigkeit lässt sich mit digitalen Kraftmessgeräten erzielen – diese sind jedoch nicht billig. Um die ungefähren Werte für Stillstands- und Betriebsdrehmoment zu ermitteln, ziehen Sie Ihren Roboter ohne Motoren mit der Federwaage eine ebene Fläche entlang. Wenn der Buggy steht, erhöhen Sie die Zugkraft, bis er gerade beginnt zu rollen, und notieren den Wert, den die Waage anzeigt. Dadurch erhalten Sie den Wert für die Kraft, die zur Überwindung der Haftreibung nötig ist. Wenn Sie den Roboter mit der gewünschten Betriebsgeschwindigkeit weiterziehen, können Sie die niedrigere, während des Betriebs nötige Kraft ablesen. Die Sache wird dadurch komplizierter, dass eine in Gramm/Kilogramm kalibrierte Waage das Gewicht misst. Glücklicherweise lassen sich kg durch Multiplikation mit der Konstante 9,81 m/s2 (die Beschleunigung durch die Schwerkraft) in Newton umrechnen.
Drehmoment berechnen
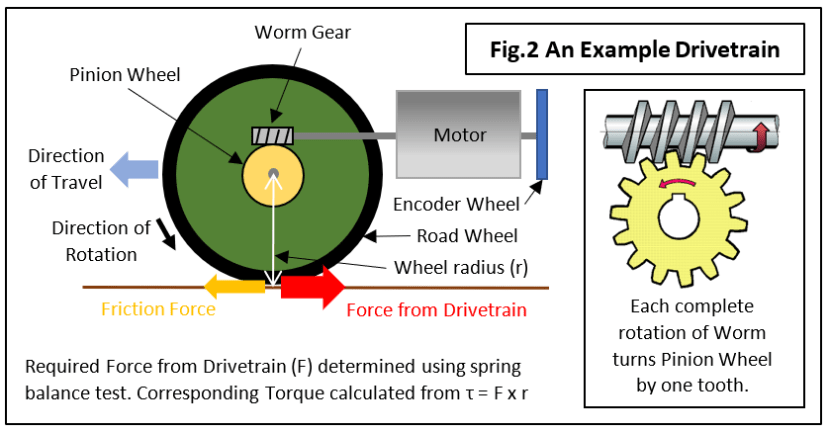
Unser Experiment hat einen Schätzwert für die lineare Kraft ergeben, die zum Bewegen des Roboters erforderlich ist und für die ein geeigneter Motor gefunden werden muss. Das Problem besteht darin, dass wir zwar die benötigte lineare Kraft kennen, die Motoren aber Drehkraft bzw. das Drehmoment τ erzeugen. Genau dies ist der Zweck der Laufräder: Die Umwandlung der Drehbewegung in eine lineare Bewegung des Roboters über den Boden. Ein Beispiel für den Antriebsstrang eines mobilen Roboters, bei dem die Motordrehzahl mithilfe eines Schnecken- und Ritzelgetriebes auf eine zur praktischen Nutzung geeignete Laufradgeschwindigkeit heruntergebrochen wird, ist in Abb. 2 dargestellt. Nun gilt: Raddrehmoment in Newtonmetern = Lineare Kraft x Raddurchmesser bzw.
τ = F x r Nm
Aus dieser Formel ergibt sich in Kombination mit der größeren Anlaufkraft, die wir gemessen haben, das Anlaufdrehmoment, das vom Antriebsstrang bereitgestellt werden muss. Mit derselben Formel ermitteln wir auch das Betriebsdrehmoment am Rad. Beachten Sie, dass es bei diesem Projekt zwei Antriebsstränge gibt – das erforderliche Drehmoment ist für jeden Motor also halb so groß wie der berechnete Wert.
Räder im Hinblick auf Geschwindigkeit oder Zugkraft auswählen
Räder für eine Mikromaus werden wahrscheinlich einen Durchmesser von ca. 3 cm haben: Für ein so kleines Fahrzeug ist dies recht viel. Es gibt eine einfache Regel, wie Sie für Ihr Projekt geeignete Räder auswählen: Groß (im Durchmesser) für hohe Geschwindigkeiten, kleiner für eine stärkere Zugkraft. Sportwagen und Mikromäuse sind auf Geschwindigkeit ausgelegt, daher die großen Räder. Schwere Nutzfahrzeuge haben relativ kleine Räder, um schwere Lasten mit (vergleichsweise) langsamer Geschwindigkeit zu transportieren. Rover für den Einsatz auf anderen Planeten bewegen sich sehr langsam und benötigen eine große Zugkraft, um Hindernisse auf unebenem Gelände zu überwinden. Die oben angeführte Gleichung zur Ermittlung des Drehmoments besagt genau dies: Durch die Verringerung des Raddurchmessers sinkt das vom Antriebsstrang benötigte Drehmoment, jedoch auf Kosten einer langsameren Fahrgeschwindigkeit. Alternativ dazu können Sie das Drehmoment des Motors zugunsten einer größeren Beschleunigung und Steigfähigkeit beibehalten.
Dies ist die einfache Formel zur Umwandlung der linearen Geschwindigkeit SL in cm/s in die Drehgeschwindigkeit SR in U/min:
SR = 60/πD x SL U/min, wobei D der Raddurchmesser in cm ist.
In unserem Beispiel mit SL = 40 cm/s und D = 3 cm ergibt sich SR = 254 U/min. Das ist es, was wir brauchen!
Leistung und Wirkungsgrad
Ein Datenblatt für einen Dauermagnet-Gleichstrommotor enthält manchmal Diagramme, in denen die mechanische Leistung (an der Welle) und der Wirkungsgrad in Abhängigkeit von der Drehzahl dargestellt werden (Abb. 1). Diese Darstellungen können irreführend sein, da sie jeweils eigene Werte für die vertikale Achse erfordern und die Beziehung zwischen den einzelnen Kurven schwer zu erkennen ist. Aus diesem Grund sind die Achsen in meinem Diagramm zwischen 0 und 100 % des Maximalwerts kalibriert.
Der Wirkungsgrad eines Motors beschreibt das Verhältnis zwischen der mechanischen Ausgangsleistung (dem Teil, das die gewünschten Arbeiten ausführt) und dem elektrischen Leistungseingang. Aus verschiedenen Gründen beträgt er nie 100 %:
- Der Draht, aus dem die Motorwicklungen bestehen, ist kein perfekter Leiter, sondern hat einen kleinen Widerstand R in Ohm. Der Energieverlust in Form von Wärme lässt sich mit der Formel PI= I2R berechnen, wobei I der Ankerstrom ist.
- Der Rotor wird durch den Luftwiderstand beeinträchtigt und dadurch entsteht ein Leistungsverlust. Dieser ist bei Drehzahl Null offensichtlich Null, wächst aber proportional zur dritten Potenz der Drehzahl.
- Weitere Verluste entstehen durch Reibung zwischen Kugellager und Bürste sowie Wirbelströme im Eisenkern.
Die Kurve für die Wellenleistung im Verhältnis zur Drehzahl lässt sich anhand folgender Gleichung darstellen:
PS = τ x ω Watt, wobei τ = Drehmoment in Nm und ω = Drehzahl in Radianten/s ist.
Abb. 1 zeigt, dass die maximale Wellenleistung bei halbem Stillstandsdrehmoment erreicht wird. Im obigen Beispiel habe ich bereits erwähnt, dass die effizienteste Betriebsdrehzahl nahe am Leerlaufwert liegt. Aber warum nicht bei 50 %, was der maximalen Ausgangsleistung entspricht? Um das festzustellen, benötigen wir ein Diagramm, das den Wirkungsgrad im Verhältnis zur Drehzahl darstellt:
Wirkungsgrad = PS/(PS+PL) x 100 %, wobei PS = Wellenleistung und PL = Leistungsverlust durch I2R und Luftwiderstand ist.
Die resultierende Kurve für den Wirkungsgrad zeigt für diesen bestimmten Motor einen schönen linearen Anstieg von Null auf ca. 85 %, bevor der Wert abrupt abfällt, bis er bei der Leerlaufdrehzahl beinahe Null erreicht. Ließe man den Leistungsverlust durch Luftwiderstand außer Acht, so würde der Wirkungsgrad weiter steigen, bis er bei der Leerlaufdrehzahl einen Endwert von ca. 95 % erreicht – nicht 100 %, da auch bei maximaler Drehzahl noch ein kleiner Strom fließt. Den abrupten Abfall verursacht der Energieverlust durch den Luftwiderstand, da der auf den Rotor einwirkende Luftwiderstand bei Annäherung an die maximale Drehzahl enorm zunimmt.
Den optimalen Bereich auswählen
Der beste Kompromiss zwischen nutzbarer Wellenleistung und ungenutzter Energie liegt an oder kurz vor der Spitze der Kurve für den Wirkungsgrad. Der Dauerbetrieb am Punkt der maximalen Wellenleistung oder in der Nähe davon kann aufgrund der Überhitzung durch I2R-Verluste problematisch sein. Wenn dies wahrscheinlich erscheint, müssen thermische Berechnungen durchgeführt werden, um sicherzustellen, dass die maximale Betriebstemperatur nicht überschritten wird.
Einen Regelkreis einbauen
Alle hier aufgeführten Berechnungen beruhen auf der Annahme, dass der Motor mit seiner Nennspannung betrieben wird und dass Stillstandsdrehmoment und Leerlaufdrehzahl den Maximalwert erreichen. Bei Anwendungen mit variablem Lastmoment, wenn z. B. ein mobiler Roboter auf eine Steigung trifft, ändert sich die Geschwindigkeit entsprechend. Da dies wahrscheinlich nicht erwünscht ist, wird ein Regelkreissystem mit einem Geschwindigkeitsmesser benötigt, der durch Steigerung der Klemmenspannung das Drehmoment erhöht, bis die eingestellte Geschwindigkeit erreicht wird. Das ist natürlich nur möglich, wenn die Geschwindigkeit auf ebenen Flächen mit weniger als der maximalen Nennspannung erreicht wird, damit Potenzial nach oben bleibt, wenn Steigungen zu überwinden sind. Weitere Informationen finden Sie in diesem Artikel zur PID-Steuerung.

