Pytorch深度學習框架X NVIDIA JetsonNano應用-torch.nn實作 (繁體)
关注文章你觉得这篇文章怎么样? 帮助我们为您提供更好的内容。
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
你觉得这篇文章怎么样?
|
作者 |
嘉鈞 |
|
難度 |
理論困難,實作普通 |
|
材料表 |
|
上次的教學教到如何刻一個線性回歸,這次的教學將使用 torch.nn 由官方提供的各種模組,來加速刻程式的速度,也因為 torch 將各種模型、演算法都包好,使用者在開發上也會更輕鬆,我們將完成。
- 透過nn建置 Linear Regression
- 激勵函數(Activation Function)
- 建置一個神經網路
透過torch.nn建置 Linear Regression
我們將使用上一次的數據圖來改建Linear Regression,第一步我們將學習使用nn.Linear,這個模組其實就是之前的線性方程 ,其中有兩個引數各別代表是輸入維度、輸出維度,使用它將可以避免掉手動建置權重跟偏差,torch會自動幫你算好對應的矩陣形狀,可以注意到W的形狀是 [4, 3],主要是因為其實 Linear的函數會先針對 W做轉置才會與x進行點積,為了符合y的大小。
嘗試改造過後你會發現其實沒減少太多程式碼 (如下圖):
因為 weights跟bias 都要「個別」更新,所以就佔掉很多行數,torch的nn.Module可以透過 .parameters() 跟 .zero_grad() 來一起搞定參數更新,首先需要先建立一個類別並且繼承nn.Module,標準格式是 init 裡面通常會放神經網路的架構,而forward就是向前傳遞該怎麼傳遞(哪一層接到哪一層的概念),宣告完模型的類別記得要實例化該模型
|
原本的程式 |
更改後的程式 |
|
|
|
你會發現在更新參數的時候更簡潔了,但是其實還可以更簡潔一點,這時候就要用到optim優化器去協助我們模型訓練,它將可以取代掉我們原先「手動更新」的部分,首先需要先導入函式,挑選你要的優化器並且告知那些參數是要訓練的,還要告知學習率是多少。
宣告完之後原本落落長的程式碼只要兩行就搞定了:
|
原本的程式 |
更改後的程式 |
 |
 |
接下來是訓練流程的比較,你看,是不是更清晰了?
|
原本的程式 |
更改後的程式 |
 |
 |
完整程式碼如下:
那在程式端我們很直觀的理解到優化器可以減少程式碼的量,但是為什麼要用優化器呢?這邊要稍微帶一點基礎觀念,已經很了解的讀者們可以先跳過~
我們之前在對Loss做偏導數求梯度再乘上學習率去更新參數的方法叫做梯度下降 ( gradient descent ),使用各種參數的梯度值去最小化或最大化損失函數的數值,而optimizer就是梯度下降的優化方法;主要有兩個面向,第一個是計算梯度下降的方向 (偏導數),第二個是找到適合的學習步長 (學習率,Learning Rate,以下簡稱 lr );你會發現我們的程式都是固定的學習率,而這又會有什麼問題呢?下圖是所有有可能出現的參數對應出的loss示意圖,而我們的目的是要走到山谷谷底,計算梯度等於是告訴你谷底的方向,學習率則是你每次跨出的步長,你可以注意到如果步長過大或不變的時候,都有可能走不到最谷底,而步長太小又會走太慢,甚至迭代次數跑完了還沒到達目的地。
圖片來源:李弘毅-ML Lecture 3-1: Gradient Descent
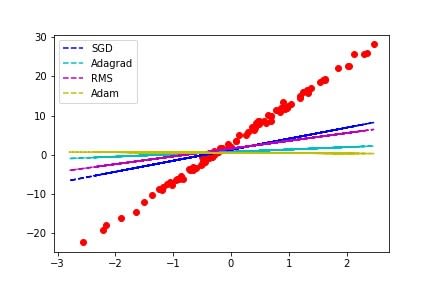
所以控制學習率是梯度下降很重要的環節,目前常出現的演算法有SGD (Stochastic gradient descent)、Adagrad、RMSprop、Adam,詳細的差別就不多說了,大家可以自己去查資料,以下簡單做個測試,epochs為100次,lr設0.1,我們來觀察看看3種不同的優化器的結果:
雖然Adam是目前看似最強大的演算法,但是在這個僅50次迭代的簡單問題中 SGD收斂是最較快且正確的;所以挑選優化器也是一門學問,有時候不是用上最強的演算法就能符合自己的需求,不過如果你覺得太複雜的話還是可以直接套用 Adam啦,畢竟他簡單或複雜的問題都可以獲得不錯的結果!
激勵函數(Activation Function)
通常在處理較複雜 ( 非線性 ) 問題的時候就需要用到激勵函數,文章前面提到的Linear Regresion就是去解決線性的問題,可以用一條直線預測出數據的分布或趨向,而遇到非線性的則稱為 Logstic (non-linear) Regression,下圖為簡單的差別,除了第一個可以用線性回歸解決其餘都不太可行。
神經網路模型遇到的問題通常都是比較複雜的,所以大部分必須採用激勵函數來協助模型解決複雜問題,下圖是常見的激勵函數,x軸是輸入y軸是輸出;
圖片來源:Tim Wang-【ML09】Activation Function 是什麼?
Pytorch使用激勵函數一樣在torch.nn中呼叫即可,程式碼如下圖可以再對照上面的圖做確認,像是原本的數值是[ -1. , 1. , 0. ],經過 Sigmoid函數就變成了 [ 0.26 , 0.73 , 0.5 ] ,因為Sigmoid會將數值 ( x ) 縮限在 [ -1 , 1 ] 之間,最初我在理解激勵函數就是直觀的認為目標是要將輸出縮限到對應的需求,之後才去理解線性與非線性、運算量的問題。
建置一個神經網路
我們先創造一個稍微複雜一點的數據,然後嘗試建置一個沒有激勵函數的神經網路模型並迭代6000次看看效果,接著建置含有激勵函數的神經網路模型再比較一次。
建置多層的神經網路其實非常簡單,我們一樣使用nn.Module來建置,主要的差別在於__init__的部分需多宣告幾層,而forward的部分需要將其連接在一起;這邊我將激勵函數寫成方便改變的方式,並且將是否使用激勵函數、使用哪個激勵函數寫在一起,而我的範例提供ReLU、Tanh兩種訓練結果:
訓練的程式碼如下:
第一次訓練的時候,我不使用激勵函數來訓練神經網路,也就是說現在的神經網路只能解決線性的問題,可以從下圖觀察到該模型沒辦法收斂到正確答案:
接著我使用ReLU、Tanh來嘗試,你會發現在曲線的地方有成功的收斂了,你們可以利用前面提供的激勵函數圖表來嘗試猜猜看哪一個ReLU?
答案是左邊是ReLU,你可以注意到沒有y值是負的,原因就是ReLU會將輸出其收斂在 [ 0 , n ] 之間 ( n表示任意數 ),所以在我們這個案例中使用 ReLU可能就不是個好選擇,反觀Tanh是將數值收斂在 [ -1, 1 ] 之間,所以在我們的案例中使用它就不會遇到任何問題,由此可知選擇激勵函數也是一門大學問了,如果你的輸出要收斂到哪裡就該選擇哪個又或者是多個選項輸出的話就該選擇maxout、輸出對與錯就使用sigmoid等等。
結語
看完了這篇你已經學會線性回歸 ( linear regression) 與邏輯斯回歸 (logistic regression),利用PyTorch建置神經網路的基礎也已經都摸透了,下一篇將稍微進階一些來玩捲積神經網路並做一個小專案。























评论