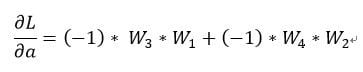Pytorch深度學習框架X NVIDIA JetsonNano應用-線性回歸與實作 (繁體)

深度學習的框架有很多種，Tensorflow、PyTorch、Mxnet、Theano等等的，其中最大眾的算是Google的Tensorflow，但還有一大部分的使用者是透過PyTorch來開發深度學習，今天我們就來介紹並使用PyTorch這款深度學習套件並且使用torch做個簡單的線性回歸；這篇文章的對象是對於深度學習已經稍微有點概念想自己建構神經網路模型的人。

安裝

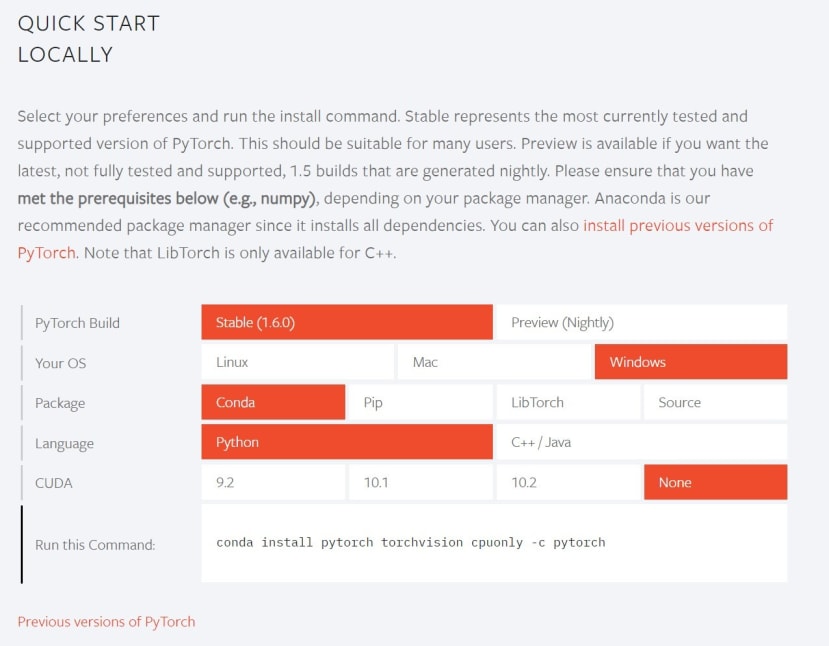
安裝方法非常的簡單，對於Nvidia的相容度也很高只要選取對應的CUDA版本即可使用GPU訓練，不過我們基本上都是使用邊緣裝置所以今天帶大家安裝CPU的版本；直接前往PyTorch的官網進行選取版本https://pytorch.org/

這邊我們安裝了一個名為torch的 Anaconda虛擬環境

>	conda create --name torch python=3.7 -y  
>	conda activate torch  
>	conda install numpy jupyter -y  
>	conda install pytorch torchvision cpuonly -c pytorch 

其餘套件，numpy是數學運算很好用的函式庫，支援大量維度的矩陣運算，也是神經網路數據處理的好工具而matplotlib是Python程式語言及其數值數學擴展包 NumPy的可視化操作界面。

>	conda install numpy matplotlib -y

我的每個套件版本如下圖：

安裝好之後我們可以使用Jupyter-notebook來練習PyTochScript，直接在終端機中輸入指令即可：

>	jupyter notebook

可以直接在jupyter-notebook中新增Python3的程式語言，在這邊可以直接使用 import 將 pytorch導入，需要注意的地方是導入套件的名稱是「torch」不是「pytorch」，在jupyter中執行只需要點選欲執行的Block並按下Shift+Enter，若沒有報錯代表能夠成功執行。

基礎函式

1. 張量

張量是深度學習的基本元素，轉成張量才方便神經網路去做運算，因為除了有規律性之外還方便GPU進行大量地平行運算；張量的定義在各種領域上都有不同的見解，這邊廣義的理解就是任何維度的資料，有時候可表示在一張圖上所有的座標點，有時候也可以表示圖片所有pixel的RGB數值，甚至一維向量在這裡也可以轉換成張量。而PyTorch 自稱是深度學習界的 Numpy，會這樣說代表它的操作幾乎跟Numpy差距不大。

2. 生成張量

使用方法與函式名稱與Numpy相同，宣告也非常簡單易懂。

3. 從Numpy轉換成Tensor

PyTorch的優勢在於數據轉換非常的方便，有時候我們需要將訓練的參數提取出來查看，像是特徵圖如果是張量的形式是無法被OpenCV或PIL顯示出來的，這時候就需要將張量轉換回Numpy，其中如果是張量的話會在印出來的時候於最前面顯示。

4. 將Tensor 放入GPU以及提取成Numpy

下圖沒有提到的是，如果張量在GPU當中訓練，需要先使用 .detech() 凍結該張量，因為怕影響到神經網路的訓練。

5. 合併、塑形、最大值、維度相加

這幾種技能是深度學習非常常用到的關鍵，在這邊使用的方法跟Numpy一樣，只是函式的名稱不同而已。

6. PyTorch的Autograd

6-1 計算圖 (Computation graphs)　原理

介紹之前先來帶點有關計算圖的基礎觀念，如果已經會了的人可以考慮跳到第二小節程式的部分；計算圖存在的意義是為了讓程式更方便計算，從計算的層面來看，神經網路的計算主要分成兩個部分：

1. Forward (向前傳遞)：計算Loss損失函數數值
2. Backward (反向傳遞)：用於計算梯度

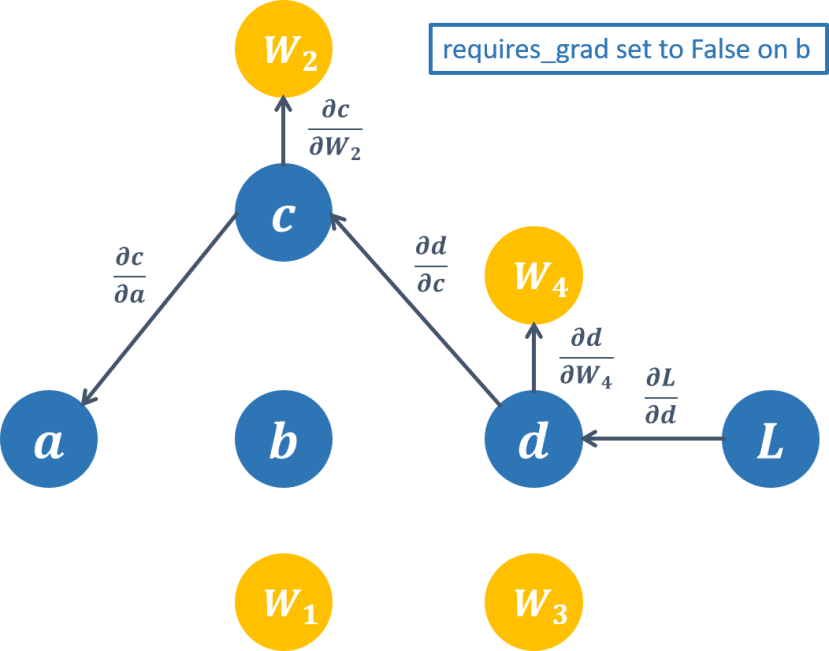
圖6.1 神經網路模型

圖6.2計算圖的節點就像個函數

計算圖中向前傳遞的計算方式非常的簡單，每個節點都可以當作是一個簡單的函數，而計算完的結果如下，這邊假設正確輸出是10，L是模擬計算損失函式：

如果我們去針對該模型的起始a去計算偏導數的話如下：

可以發現這些計算都是依循了「鏈鎖律」，複雜的函數都是由簡單的函數所構成對於這個神經網路模型手動計算很簡單，但是當神經網路很複雜的時候就不適合這樣去計算，所以才產生了計算圖的方式，讓電腦按照順序去計算所有變量的梯度；由於反向傳遞也符合鏈鎖律的法則，所以我們可以針對個別的運算去做偏導數再做合計，理論上會獲得一樣的結果。

圖6.3 反向傳遞的時候針對個別的函數進行微分

假如我們現在計算整個函數 L 對 a 的導數，有幾個重點：

1. 我們需要先找到整個函數可以從L 走到 a 的所有路徑，總共兩條
2. 將其路徑上所有偏導數相乘，記得只有數學運算的部分也就是邊條的部分

所以最後的結果會跟我們手動求偏導的結果是一樣的：　

整理一下會發現，結果竟然一樣：

6-2 PyTorch的Auto grad framework

為了讓PyTorch知道這些張量是要進行反向傳遞的，我們必須再宣告的時候使用 requires_grad，讓這些張量的計算保存在計算圖當中。順帶一提，requires_grad的預設值是False。

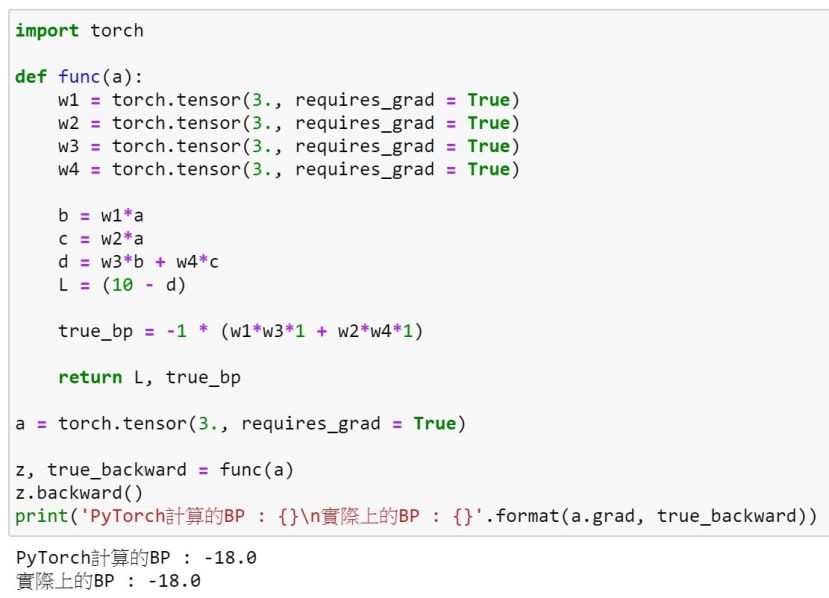
我們先用一個很簡單的範例來測試反向傳遞，在PyTorch中我們使用 backward函數來進行反向傳遞，它會自動幫我們算好並且使用 grad 將其計算後的結果取出，記得backward的對象是最後的輸出而grad的對象是預計要訓練的權重。

接下來我們透過先前所說的範例來進行反向傳遞，可以看到結果是正確的。

6-3 PyTorch凍結權重

在神經網路的訓練中，有些人會刻意凍結某些層讓模型不會訓練到那些參數，遷移學習或是生成對抗都會用到該技術；在Tensorflow的作法需要使用到freeze() 的函數，而PyTorch可以將required_grad() 設定成False或是使用torch.no_grad() 這個函數。

實作：線性回歸 (Linear Regression)

前面已經將大部分基礎的PyTorch給介紹完了，接下來可以建置一個簡單的線性回歸試試看，首先機器學習中有分線性回歸與非線性回歸兩種

，建立的步驟如下：

1. 建立最基本的線性模型，例如 : y = w * x + b
2. 設定要訓練的數據 ( 輸入 x、權重 w、偏差b以及輸出 y )，我們選擇先將 w、b預設 [ 10. , 3. ] 方便觀察電腦是否收斂到跟預設值一樣。

3.我們的目的是要讓模型可以慢慢學習到正確的權重 ( w )，所以這邊我們利用 randn 來隨機產生權重 ( w_ )，讓模型自己更新成正確的權重；並且我們宣告一組新的 x 用來預測 ( 測試資料 )。

4.設定超參數，目前先定義了「迭代次數」、「紀錄時間」、「學習率」。

5.隨機生成的權重 ( w_ ) 會計算出一組新的答案 ( y_ )。我們會計算新的 y_ 跟正確解答 y 的「差距」也就是Loss，我們可以透過 loss知道現在對於模型來說是否越來越接近正確解答；而我們使用的方法是MSE。

6.Loss 的部分需要進行反向傳遞來獲得梯度，讓模型知道還差多遠、朝哪個方向走才會逼近解答。

7.接下來就要更新權重，通常會設置一個學習率來調整更新的步伐大小。這邊要注意的事，由於 PyTorch 每次呼叫參數都會將數據追蹤到計算圖中，為了防止重複運算我們使用 no_grad，並在其底下更新權重 ( w_ )。

8.新的權重 ( w_ ) 就會獲得新的答案 ( y_ )，也會有新的梯度 ( w_.grad )，所以記得要將梯度給清除，不然會將舊的累加上去。

完整程式碼以及視覺化結果如下：

可以發現因為模型簡單進行50次迭代就能收斂的很好，為了更好的觀察我也做了視覺化，可以注意到每次迭代都有確實往Ground Truth收斂：

結語

整篇文章下來相信你已經學會如何用PyTorch製作一個LinearRegression了，不過還有一個LogsticRegression還沒實作，這部分會在下一篇中也會一併介紹，此外還會教大家使用torch.nn改造這篇最後的程式，torch.nn是torch幫大家打包好的模組，裡面有各種函數可以調用，建置神經網路的全連接層、捲積層等，還有激勵函數、優化器等，你將會發現torch建置神經網路的快速跟強大。

參考

• 深度學習新手村：PyTorch入門
• 深度學習入門之PyTorch
• 李弘毅PyTorch教學投影片PyTorch Introduction by Chi-Liang Liu
• PyTorch 101, Part 1: Understanding Graphs, Automatic Differentiation and Autograd