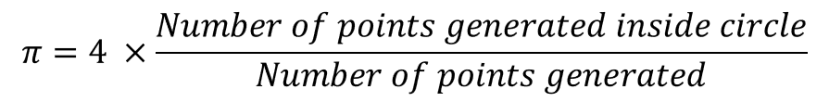À quel point un algorithme peut-il s'exécuter plus rapidement dans une matrice FPGA plutôt qu'un processeur ?
Suivez l'articleQue pensez-vous de cet article ? Aidez-nous à vous fournir un meilleur contenu.
Merci! Vos commentaires ont été reçus.
There was a problem submitting your feedback, please try again later.
Que pensez-vous de cet article ?
Un FPGA (Field Programmable Gate Array) est un réseau de portes logiques programmées par le hardware afin d'exécuter une tâche spécifiée par l'utilisateur. Les FPGA présentent l'avantage d'incorporer un parallélisme permettant d'effectuer simultanément de nombreux calculs ou instructions, ce qui améliore considérablement la vitesse de calcul du système par rapport aux plates-formes construites sur un processeur. Grâce à ses ressources intégrées à haute vitesse, telles que les tranches DSP et les mémoires rapides, les FPGA sont maintenant également utilisés pour l'accélération des algorithmes.
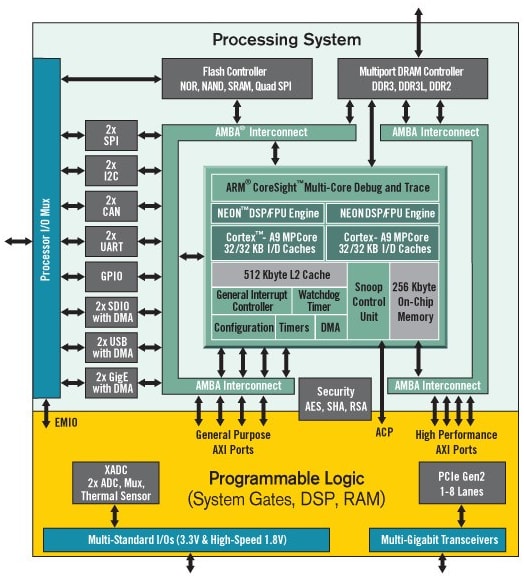
Ce projet compare la vitesse d'exécution d'un algorithme d'estimation Pi sur un système FPGA, et celle à laquelle le même algorithme s'exécute sur un processeur. En l'occurrence, un algorithme d'estimation Pi de Monte Carlo s'exécute à la fois sur le processeur et la structure FPGA du Digilent Cora Z7 Zynq-7000, en option simple cœur et double cœur, pour le développement du SoC ARM/FPGA. L'architecture Xilinx Zynq-7000 incorpore un processeur ARM Cortex-A9 à 667 MHz, simple ou double cœur, avec un FPGA Xilinx de série 7.
Architecture du Zynq APSoC
Les variantes produit du Cora Z7 sont respectivement nommées Cora Z7-10 (184-0484) et Cora Z7-07S (184-0456) . Leur seule différence réside dans la capacité de la pièce Zynq. Le large éventail d'interfaces matérielles du Cora Z7 – allant d'un PHY Ethernet 1 Go aux convertisseurs analogique-numérique et aux broches d'entrée / sortie à usage général – en fait une plateforme idéale pour le développement d'une grande variété d'applications embarquées.
| Variante du produit | Cora Z7-10 | Cora Z7-07S |
|---|---|---|
| Composant Zynq | XC7Z010-1CLG400C | XC7Z007S-1CLG400C |
| Nombre de cœurs du processeur ARM | 2 | 1 |
| 1 ADC sur puce MSPS | Yes | Yes |
| Tables de reherche (LUTs) | 17,600 | 14,400 |
| Flip-Flops | 35,200 | 28,800 |
| Tranches DSP | 80 | 66 |
| Blocage de RAM | 270 KB | 225 KB |
| Carreaux de gestion de l'horloge | 2 | 2 |
Plate-forme Cora Z7 Zynq 7000
Estimation de Pi par la méthode Monte Carlo
Il existe de nombreux sites Internet expliquant l'estimation de Pi par la méthode de Monte Carlo ; vous pouvez par exemple consulter ce site web. Ce procédé consiste à générer un grand nombre de points aléatoires, puis de voir combien tombent dans le cercle délimité par l'unité de mesure carré. L'aire d'un carré est de 1, tandis que celle du cercle est de pi / 4, puisque le rayon est de 0,5. Avec un grand nombre de points aléatoires (x,y),
Pour mettre en œuvre l'algorithme, il suffit de générer un point aléatoire (x, y) puis de vérifier si sa distance par rapport à l'origine (x,y) est inférieure ou égale à 1 (x2 + y2 <= 1). Si oui, vous incrémentez le nombre de points apparaissant à l'intérieur du cercle.
Exécuter l'algorithme sur un processeur ARM sous Linux
Le tutoriel vous apprend à démarrer Linux sur un processeur ARM Cora Z7. Vous pouvez ensuite utiliser le langage de programmation Go pour estimer la valeur de Pi par la méthode de Monte Carlo. Ce dont vous aurez besoin, c'est d'un système Ubuntu 16.04.3, de Xilinx Viavdo 2017.4, Petalinux et Golang. Golang peut être installé via apt-get, mais les autres outils doivent être téléchargés depuis le site web de Xilinx. Vous devez utiliser Petalinux pour démarrer sous Linux.
Le tableau ci-dessous indique le temps nécessaire à chacune des variantes de Cora Z7 pour traiter cent mille échantillons de Monte Carlo.
Exécuter l'algorithme sur du matériel FPGA
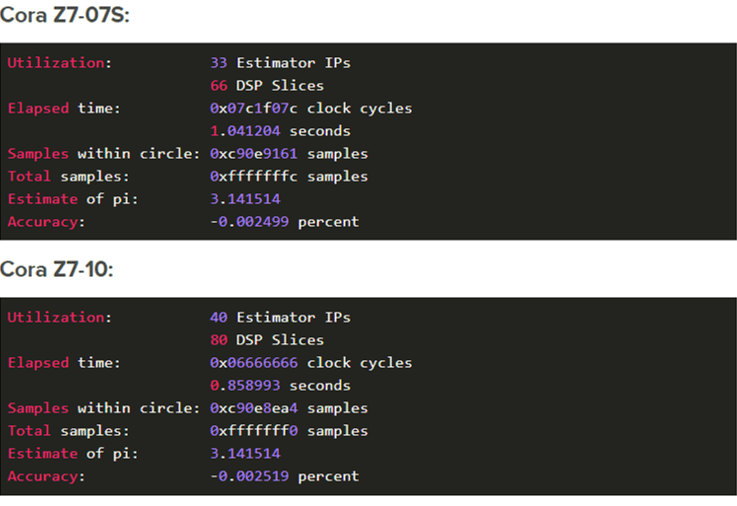
Le tutoriel vous montre comment construire l'algorithme dans la logique FPGA. La structure du FPGA contient des éléments appelés « tranches de traitement numérique du signal » (DSP slices). Dans le cas de l'exécution de la méthode de Monte Carlo, vous devez effectuer deux opérations de multiplication (x*x et y*y). Tant que le résultat de chaque opération de multiplication est inférieur à 48 bits, vous ne devez utiliser que deux des tranches DSP de Cora par instance de code exécutant la simulation de Monte Carlo. Les échantillons aléatoires sont créés en utilisant un registre décalé à rétroaction linéaire (LFSR), avec valeur de départ fournie par le contrôleur. L'horloge de l'ensemble du système est de 125 MHz. Choisissez d'exécuter autant d'échantillons qu'un entier de 32 bits puisse contenir.
Voici les résultats générés par chaque variante de Cora :
FPGA ou processeur?
Tandis que la plus lente des deux variantes de Cora Z7 était capable de traiter un nombre complet d'échantillons sur un entier de 32 bits en approximativement une seconde, la plus rapide ne gérait que cent millions d'échantillons en 1,8 seconde, sous Linux. En d'autres termes, la version accélérée par le matériel de l'algorithme était 77 fois plus rapide. La conception du FPGA permet de traiter neuf échantillons Monte Carlo par cycle d'horloge (soit un cycle d'horloge toutes les huit nanosecondes).