Blockchain Primer - Partie 1
Suivez l'articleQue pensez-vous de cet article ? Aidez-nous à vous fournir un meilleur contenu.
Merci! Vos commentaires ont été reçus.
There was a problem submitting your feedback, please try again later.
Que pensez-vous de cet article ?
Si l'on devait se fier au battage médiatique, la blockchain mettrait fin à la maladie, à la pauvreté et à la faim, inaugurant ainsi une ère nouvelle et magnifique de paix mondiale. Si elle n'est peut-être pas la solution miracle vantée par certains services marketing, elle n'en reste pas moins un outil fiable apportant une solution crédible dans de nombreuses applications.
Pour déterminer quelles applications conviennent (ou non) à la blockchain, il est utile de connaître la théorie qui la sous-tend ainsi que sa mise en œuvre. Dans cet article, nous tenterons de faire la "synthèse" des connaissances nécessaires, afin de vous permettre de prendre vos propres décisions vis-à-vis de cette technologie passionnante.
Genèse
Contrairement à l'opinion populaire, la blockchain n'a pas surgi de l'esprit de Satoshi Nakamoto pleinement formée et armée de pied en cap, telle une Athéna moderne.
Le concept initial remonte à une publication de 1991 par Stuart Haber et W. Scott Stornetta intitulée 'How to Time-Stamp a Digital Document' ("Comment horodater un document numérique") qui cherchait à résoudre le problème de l'horodatage des données numériques de façon à ce qu'il soit impossible d'antidater (ou de post-dater) les données une fois estampillées.
À cette époque, tout ce qui relevait du numérique pouvait facilement être usurpé, cela représentait donc un dilemme pour les ingénieurs qui souhaitaient utiliser la technologie réseau pour mettre en place toutes sortes de processus, du travail collaboratif à distance aux transactions numériques.
Satoshi Nakamoto (quelle que soit l'identité réelle de cette personne) a mis à profit les concepts de sécurité développés par Haber et Stornetta lors de la création de Bitcoin.
.
Bloc Genesis
Il existe un certain nombre de définitions vagues de ce que constitue une blockchain, mais la définition que nous allons utiliser est la suivante :
"Une liste sans cesse croissante d'enregistrements, appelés blocs, qui sont liés ensemble et sécurisés par cryptographie."
Les enregistrements sont liés et sécurisés en utilisant une technique appelée hachage. Nous nous attarderons d'avantage sur ce point par la suite, mais pour l'heure représentez-vous l'algorithme de hachage comme quelque chose qui prend "l'empreinte digitale" d'un bloc de données. Tout comme une empreinte digitale, chaque hachage est (quasi) unique.
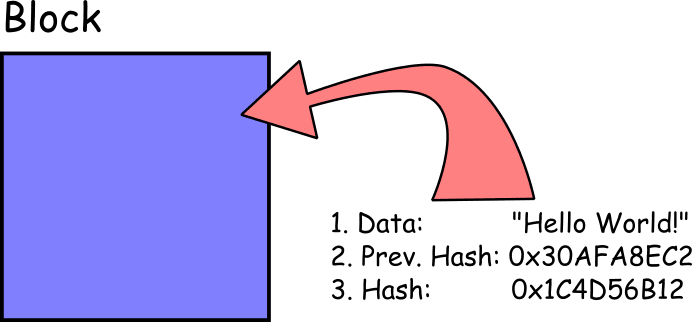
Un bloc viable contiendra au moins 3 choses :
Les "données" peuvent être constituées d'à peu près tout ce que vous pouvez imaginer, mais il s'agit en général d'un petit ensemble d'éléments, semblables à ceux que l'on aurait pu inscrire en l'espace d'une ligne dans un registre en papier. Cela pourrait inclure, par exemple, des informations sur une transaction financière, les coordonnées GPS de l'emplacement d'un conteneur ou le rythme cardiaque et la pression artérielle d'un patient à l'hôpital. Elles peuvent aussi constituer une valeur nulle ou vide, attestant qu'aucune donnée n'a été enregistrée à un moment précis.
Le "hash" est la valeur de hachage du contenu du bloc. Dans le cas présent, il constitue la valeur de hachage des données (data) et du hash précédent (prev.hash).
Le "hash précédent" est ce qui nous permet de lier les blocs au plan cryptographique, en commençant par le premier bloc, appelé "Bloc Genesis". Le Bloc Genesis représente un cas particulier et n'aura pas de hachage précédent étant donné qu'il est le premier bloc de la chaîne :
Ce lien cryptographique au bloc précédent confère à la chaîne une propriété essentielle. Si les données dans le bloc 1, par exemple, ont été altérées d'une quelconque manière, cela modifiera la valeur de hachage pour ce bloc. La nouvelle valeur de hachage pour le bloc 1 ne correspondra plus à la valeur de "hash précédent" stockée dans le bloc 2 et pourra donc être facilement détectée et signalée, afin que la modification soit refusée.
Cet enchaînement particulier des blocs est ce qui permet d'assurer l'intégrité des données stockées.
À cette étape, deux questions peuvent se poser : "ne serait-il pas possible de falsifier la valeur de hachage ?" ou "ne pourrait-on pas parcourir toute la chaîne et modifier les valeurs des "hash précédents" afin de dissimuler l'effraction ?"
Afin de comprendre pourquoi ces deux propositions sont impossibles sur le plan des calculs, il nous faut explorer plus avant la nature des algorithmes de hachage.
Critères d'un algorithme de hachage
Pour qu'un algorithme de hachage soit efficace dans une blockchain, il doit répondre à cinq critères :
- Déterministe : l'entrée de données identiques produira toujours la même valeur de hachage.
- Unidirectionnelle : les données originelles ne peuvent pas être reconstituées à partir du hash.
- Effet d'avalanche : le plus petit changement appliqué aux données originales résulte en un hash de sortie totalement différent.
- Calculs rapides : l'application de l'algorithme à un bloc de données nécessite un nombre minimal de cycles de processeur, permettant d'effectuer les calculs très rapidement.
- Tolérance aux collisions : lorsque les ensembles de données excèdent l'ensemble des combinaisons possibles de l'algorithme, un hash peut se trouver réutilisé : c'est la collision. Cet événement est considéré comme extrêmement rare et l'algorithme ne peut pas autoriser des collisions forcées qui permettraient le trucage de données.
Un algorithme de hachage qui adhère à ces contraintes pourra prendre en charge des données d'entrée de n'importe quelle longueur (qu'il s'agisse de la lettre "A" ou du contenu intégral de l'encyclopédie Britannica) et rapidement générer une sortie de longueur fixe présentant une empreinte représentative des données. En théorie, un hash sécurisé est indifférenciable d'une cartographie aléatoire, et même le plus petit changement dans les données se traduira par un hash totalement différent. Vous pouvez obtenir un aperçu empirique de ce processus à l'aide de ce Générateur de Hash SHA256 en ligne.
Tables arc-en-ciel : bien que la fonction de hachage soit unidirectionnelle, ce qui signifie que les données d'origine ne peuvent pas être reconstituées à partir du hash de sortie, la nature déterministe des algorithmes, tels que SHA256 ("Secure Hash Algorithm") signifie que si vous connaissez déjà (ou pouvez réduire) les données d'entrée, vous avez la possibilité de vérifier que vous disposez des bonnes données en les comparant à une liste de hash de sortie pour les entrées connues. Le dernier rempart pour empêcher que la sécurité de vos mots de passe soit compromise est de les stocker dans un format obtenu par hachage. Toutefois, certaines tables arc-en-ciel facilement accessibles relient les mots de passe les plus utilisés à leur hash de sortie. Les hackers peuvent donc extraire les mots de passe faibles ou courants en lisant tout simplement les tables jusqu'à ce qu'ils trouvent la valeur de hachage adéquate. Un moyen de défense contre ce procédé consiste à "saler" le hash en ajoutant une suite de caractères aux mots de passe avant de procéder au hachage, afin de rendre invalides les tables arc-en-ciel les plus communes."
Résistance aux collisions
La résistance aux collisions est la véritable mesure de la force d'un algorithme de hachage. En effet, il est hautement improbable que deux entrées différentes produisent le même hash de sortie.
Selon le principe des tiroirs, si nous disposons d'une quantité n de valeurs de hachage possibles et que nous avons un nombre d'entrées supérieur à n d'une entrée (c.-à-d. n + 1 entrées), alors nous sommes susceptibles d'obtenir deux entrées avec la même valeur de hachage. Dans le cas de SHA256 cela équivaudrait à 2256 (ou 6436) valeurs de hachage possibles.
Malheureusement, l'univers est un peu plus compliqué que cela. Les lois de la probabilité, plus précisément ce que l'on appelle le paradoxe des anniversaires (ou le problème des anniversaires) nous disent que la véritable probabilité de collision pour un grand nombre est la racine carrée de n. Cela signifie que nous pouvons "seulement" calculer 2128 valeurs de hachage avant qu'il y ait une probabilité de collision.
Pour mettre le tout en perspective, si nous avons un ordinateur calculant 232 hash par seconde il faudrait compter 296 secondes avant qu'une collision ne se produise. Ce qui équivaut à environ 2,5 x 1021ans, soit bien plus que l'estimation actuelle de l'âge de l'univers (1,4 x 1010 ans) et certainement bien plus que la période de garantie d'un ordinateur tournant 24h/24.
Il y aurait plus à dire sur ces notions mathématiques que certains individus cherchent à exploiter pour organiser des attaques sur le paradoxe des anniversaires et des attaques de collision, mais en ce qui nous concerne, il suffit de savoir que, jusqu'à présent, SHA256 a résisté à ces types d'attaques.
Résumé
Nous avons examiné la théorie de base décrivant comment la blockchain relie les blocs de données ensemble pour les sécuriser en utilisant les fonctions de hachage. Dans la partie 2