RF Communication and the Internet of Things, Part 1
Follow articleHow do you feel about this article? Help us to provide better content for you.
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
What do you think of this article?
The Dark World of Radio Frequency Design
Working with Radio Frequencies can be frustrating: when you want a circuit to radiate radio waves, it won’t. When you don’t, it will. The engineer developing a tiny computer board such as Raspberry Pi is faced with the fact that PCB tracks can behave like long transmission lines at very high frequencies: stray capacitance and inductance leads to signal coupling between adjacent tracks (cross-talk), and attenuation. Worse, unless very carefully designed in terms of shape, length, source and load impedances, they act as antennas by resonating, radiating RF noise known as Electromagnetic Interference or EMI, and disrupting other electronic equipment nearby. You may have a new working design for a super Raspberry Pi killer, but if it can’t pass EMC tests then you won’t be able to sell it in most countries. That’s the trouble with RF design, if you don’t get it exactly right you may find that your project works but interferes with your TV for example, or worse, your neighbours’ TVs.
Design with Modules not Discrete Components
Take a ‘systems’ approach and build your IoT project from off-the-shelf modules and leave all the detailed component-level design to those well-schooled in the black arts of high-frequency electronics. For initial experiments and even in ‘production’ units it makes sense to use functional modules as they cost so little. For example, a simple transmitter module costing a few GBP will take in a serial data signal and put it on a high-frequency carrier ready for connection to an antenna. Of course that still leaves you with the task of selecting Transmitted RF power output, Receiver Sensitivity, Carrier Frequency, Modulation method, etc, etc to meet the main design requirement: to communicate telemetry with a specified data rate over a specified distance. Did I say it would be easy?
The Wireless Link
Fortunately, probably because the design of very high frequency wireless systems has been going on for so long there are techniques and rules to help us get a link up and running without too much fuss. In practice, if your wireless link is only a few metres long, and all in one room then many off-the-shelf solutions will probably work ‘Plug-and-Play’ without the need for any sort of design calculations. As soon as obstructions like walls and/or distances of 30 m or more are involved, then some maths may become necessary. These calculations will involve using Decibel units.
The Decibel
The decibel (dB): probably the most misused and misunderstood unit of measurement in electronics. At first glance, it might seem that RF engineers use the system of decibel units to make their craft even more impenetrable to mere mortals than it really is. RF communications systems are designed around a lot of ‘black boxes’ each with signal power going in (PIN), and signal power coming out (POUT) after some intervening processing. By representing power levels and gains/losses in logarithmic (decibel) format, multiplication is converted into addition – a whole lot easier.
If POUT is larger than PIN then the box, for example an amplifier, has a Gain. If the other way round, as in the case of a filter, then it causes a Loss. The formula for converting Power Gain (or Loss) expressed as a simple ratio to dB format is:
GdB = 10log10(G) dB where G = POUT/PIN
GdB is a positive number if POUT > PIN or a negative number if POUT < PIN
Some examples:
If G = 1 then GdB = 0 dB
If G = 5 then GdB = +7 dB
If G = 0.5 then GdB = -3 dB
The same treatment can be given to actual power levels with units of Watts or milliWatts. The same formula is used as for GdB, but the PIN value is replaced by a ‘reference value’ of 1 W if POUT is measured in Watts, or 1 mW if measured in milliWatts. This yields power values in units dBW and dBm respectively.
PdBm = 10log10(P) dBm where P is in mWatts
PdBW = 10log10(P) dBW where P is in Watts
Some examples:
If P = 1 mW then PdBm = 0 dBm
If P = 5 mW then PdBm = +7 dBm
If P = 0.5 mW then PdBm = -3 dBm
Now that we’ve defined the units used, we can go ahead and create a basic link budget for a short wireless communication channel.
Defining the Link Budget
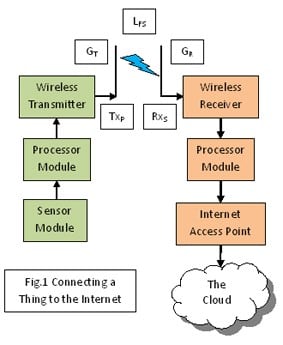
A typical Internet of Things application will involve one or more sensors attached to a data-gathering microcontroller, which is in turn linked wirelessly to an Internet Access Point using WiFi, Bluetooth or some other radio standard. (Fig.1) The link with New Horizons is different in that the range is somewhat larger and increasing at about 50000 km/hour. The basic design principles for a wireless link are the same whether it’s 1 metre or 1 billion metres long and in either case a ‘Link Budget’ needs to be created. In essence a link budget is just a simple equation that allows the designer to establish how powerful the transmitter needs to be or how sensitive the receiver to communicate over a given distance. Other factors such as noise, signalling (baud) rate, multipath effects and in the case of our moving space probe, Doppler shift are involved too. For the moment a basic budget equation for a simple short-range terrestrial wireless link organised to determine transmitter power looks like this:
TxP = RxS - GR - GT + LFS + Fade Margin dBm
where TxP = Transmitter Power (in dBm)
RxS = Receiver Sensitivity (in dBm)
GT = Transmitter Antenna Gain (in dB)
GR = Receiver Antenna Gain (in dB)
LFS = Free Space Loss (in dB)
Antenna Gain
The two antenna gains may seem rather odd: after all how can a bit of wire or rod amplify a signal? The fundamental, and entirely theoretical, antenna is an infinitely small point radiating power evenly in all directions. It’s an isotropic radiator and is our reference antenna with 0 dB gain. Real antennas don’t behave like this; a basic dipole has a radiation pattern in the shape of a doughnut rather than a sphere. It has a gain of about 2.13 dB over the isotropic antenna because all the radiated power is concentrated in the direction defined by the doughnut shape. The receiver antenna of the same type will improve sensitivity by 2.13 dB. This apparent gain only applies in certain directions. Some antenna designs such as the classic parabolic dish (e.g. Jodrell Bank radio telescope) have huge amounts of gain but focussed in a narrow beam.
Free Space Loss
Power reaching the receiver antenna falls at a rate proportional to the square of the distance travelled. This is called Free Space Loss and is calculated in dB from the formula:
LFS = 20log10(4πD/λ) dB where D = Distance and λ = Carrier Wavelength
It assumes that there are no walls or other obstructions in the path. Funnily enough this is basically the case for spacecraft communication, but is rarely the case for more terrestrial applications.
Notice that the carrier wavelength also affects the rate of signal loss. Indoors, the above equation for Loss holds true for about 6 m. After that in a building with internal walls, the signal loss increases by about 30 dB per 30 m. That’s why wifi communication can be so patchy within the home: walls are very far from transparent to radio waves. The trouble is, 2.4 GHz wifi was not developed for a domestic environment. It was designed for networking within a large open-plan office with no walls. Bluetooth has the same limitations.
Moving outside, an IoT project might involve communicating with a remote sensor up to 100m or more away. In this situation, sub-1 GHz frequencies are better because of the reduction in Free Space Loss. We are still operating line-of-sight here, and obstructions such as buildings or trees will drastically reduce the range. Mobile phone operators often fall foul of the vegetation problem, at least one designing and erecting a system of masts in winter and then…well, you can guess the rest.
Fade Margin
This component needs to be included because of the annoying habit of two or more copies of the signal arriving at the receiver out of phase with each other; sometimes so far out of phase they cancel each other out resulting in signal loss known as a Multipath Fade. The extra signal paths happen when part of the transmitted wave bounces off an object and arrives at the receiver slightly delayed relative to the direct signal. There are ways of compensating for this but for now we’ll just have to allow for fades by including an extra 20 to 30 dB in our link budget.
Noise
So far we haven’t considered the effects of electrical noise in our calculations. I’ll talk about it in Part 2 of this blog, but suffice to say noise impacts the value for Receiver Sensitivity and is related to the digital data baud rate. In general terms, this means that sensitivity falls as the baud rate rises.
Design Examples

Low data-rate, long-range version:
Using the formula for Free State Loss over 100m we get LFS = 72 dB
Use an antenna gain of 0 dB (Sometimes manufacturers assume a dipole antenna and adjust their figures to include the 2.13 dB gain. I’m assuming LPRS have done this).
From the datasheet the best Receiver Sensitivity, achieved at 1200 Baud, is RxS = -109 dBm
Finally, add a worst-case Fade Margin of 30 dB
Required Transmitter Power TxP = -109 + 0 + 0 + 72 + 30 = 7 dBm
Well there’s a bit of luck, 7 dBm is the maximum Tx power setting for the module.
High data-rate, short-range version:
Using the formula for Free State Loss over 10m we get LFS = 51 dB
Again, assume an antenna gain of 0 dB
From the datasheet the best Receiver Sensitivity, achieved at 500 kBaud, RxS = -81 dBm
Add a worst-case Fade Margin of 30 dB
Required Transmitter Power TxP = -81 + 0 + 0 + 51 + 30 = 0 dBm
So in this case you can have fast data rates within a building, and low power consumption.
The Fade Margin is pretty stiff and may be relaxed in specific situations with a fixed installation when on-site tests may be employed to establish the actual transmitter power needed for reliable communication.
CubeSat Communication
The eRIC9 module is capable of communicating over much longer distances under special conditions. One such channel largely free from obstructions and sources of multipath effects links a ground station to a satellite. The eRIC9 module was used on the Warwick University test CubeSat WUSAT-2 which achieved a height of over 80km, sending data back to Earth as it returned.
Now 80 km has a Free Space Loss of 129 dB, which even if we forget the Fade Margin leaves a deficit of 20dBm in Transmitter power. Now’s the time to bring in some antenna gain at the ground station, with perhaps a parabolic dish or Yagi array. There is less scope for large antennas on the CubeSat itself!
The key message to take away from all this theory and calculation is that it only gets you into the ball-park in terms of your design. Treat any claims for range on datasheets with scepticism because everything depends on the specific local conditions which might be ideal in one direction and hopeless in another. Part 2 looks at how Noise affects the achievable data rate with particular reference to an extreme example: getting data back from the New Horizons spacecraft at Pluto.
Part 1. IoT Communication: Decibels, Free State Losses, Link Budgets and CubeSats
Part 2. IoT Communication: Noise, Interference and Communicating with Pluto
Part 3. IoT Communication: Modulation, Coexistence, Spread-Spectrum and Chirps
Part 4. IoT Communication: Regulations and Short-Range IoT
Part 5. IoT Communication: Long-Range IoT, Datasheet Hype and Future Technologies
If you're stuck for something to do, follow my posts on Twitter. I link to interesting new electronics components and development kits (some of them available from my employer!) and retweet posts I spot about robot, space exploration and other issues.

