Pytorch深度学习框架X NVIDIA JetsonNano应用-torch.nn实作

上次的教学教到如何刻一个线性回归，这次的教学将使用 torch.nn 由官方提供的各种模块，来加速刻程序的速度，也因为 torch 将各种模型、算法都包好，用户在开发上也会更轻松，我们将完成。

• 透过nn建置 Linear Regression
• 激励函数（Activation Function）
• 建置一个神经网络

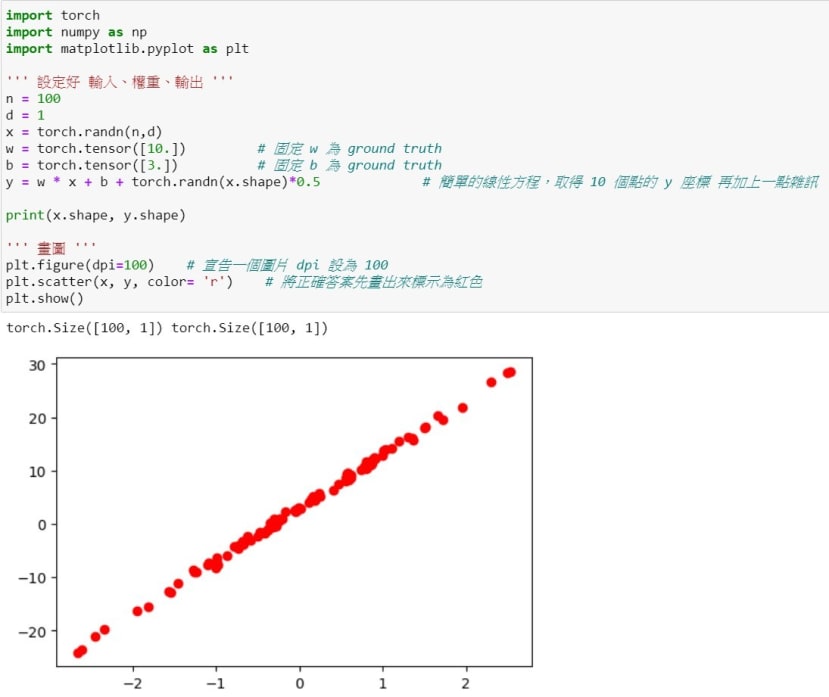
透过torch.nn建置 Linear Regression

我们将使用上一次的数据图来改建Linear Regression，第一步我们将学习使用nn.Linear，这个模块其实就是之前的线性方程 ，其中有两个自变量各别代表是输入维度、输出维度，使用它将可以避免掉手动建置权重跟偏差，torch会自动帮你算好对应的矩阵形状，可以注意到W的形状是 [4, 3]，主要是因为其实 Linear的函数会先针对 W做转置才会与x进行点积，为了符合y的大小。

尝试改造过后你会发现其实没减少太多程序代码 (如下图)：

因为 weights跟bias 都要「个别」更新，所以就占掉很多行数，torch的nn.Module可以透过 .parameters() 跟 .zero_grad() 来一起搞定参数更新，首先需要先建立一个类别并且继承nn.Module，标准格式是 init 里面通常会放神经网络的架构，而forward就是向前传递该怎么传递(哪一层接到哪一层的概念)，宣告完模型的类别记得要实例化该模型

你会发现在更新参数的时候更简洁了，但是其实还可以更简洁一点，这时候就要用到optim优化器去协助我们模型训练，它将可以取代掉我们原先「手动更新」的部分，首先需要先导入函式，挑选你要的优化器并且告知那些参数是要训练的，还要告知学习率是多少。

宣告完之后原本落落长的程序代码只要两行就搞定了：

原本的程序	更改后的程序

接下来是训练流程的比较，你看，是不是更清晰了？

完整程序代码如下：

那在程序端我们很直观的理解到优化器可以减少程序代码的量，但是为什么要用优化器呢？这边要稍微带一点基础观念，已经很了解的读者们可以先跳过～

我们之前在对Loss做偏导数求梯度再乘上学习率去更新参数的方法叫做梯度下降 ( gradient descent )，使用各种参数的梯度值去最小化或最大化损失函数的数值，而optimizer就是梯度下降的优化方法；主要有两个面向，第一个是计算梯度下降的方向 (偏导数)，第二个是找到适合的学习步长 (学习率，Learning Rate，以下简称 lr )；你会发现我们的程序都是固定的学习率，而这又会有什么问题呢？下图是所有有可能出现的参数对应出的loss示意图，而我们的目的是要走到山谷谷底，计算梯度等于是告诉你谷底的方向，学习率则是你每次跨出的步长，你可以注意到如果步长过大或不变的时候，都有可能走不到最谷底，而步长太小又会走太慢，甚至迭代次数跑完了还没到达目的地。

图片来源：李弘毅－ML Lecture 3-1: Gradient Descent

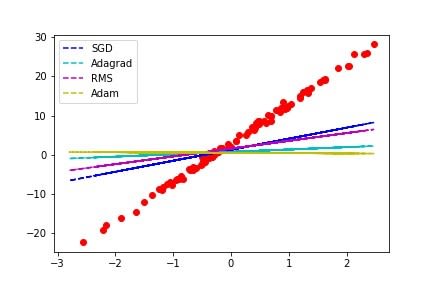
所以控制学习率是梯度下降很重要的环节，目前常出现的算法有SGD (Stochastic gradient descent)、Adagrad、RMSprop、Adam，详细的差别就不多说了，大家可以自己去查数据，以下简单做个测试，epochs为100次，lr设0.1，我们来观察看看3种不同的优化器的结果：

虽然Adam是目前看似最强大的算法，但是在这个仅50次迭代的简单问题中 SGD收敛是最较快且正确的；所以挑选优化器也是一门学问，有时候不是用上最强的算法就能符合自己的需求，不过如果你觉得太复杂的话还是可以直接套用 Adam啦，毕竟他简单或复杂的问题都可以获得不错的结果！

激励函数（Activation Function）

通常在处理较复杂 ( 非线性 ) 问题的时候就需要用到激励函数，文章前面提到的Linear Regresion就是去解决线性的问题，可以用一条直线预测出数据的分布或趋向，而遇到非线性的则称为 Logstic (non-linear) Regression，下图为简单的差别，除了第一个可以用线性回归解决其余都不太可行。

神经网络模型遇到的问题通常都是比较复杂的，所以大部分必须采用激励函数来协助模型解决复杂问题，下图是常见的激励函数，x轴是输入y轴是输出；

图片来源：Tim Wang-【ML09】Activation Function 是什么?

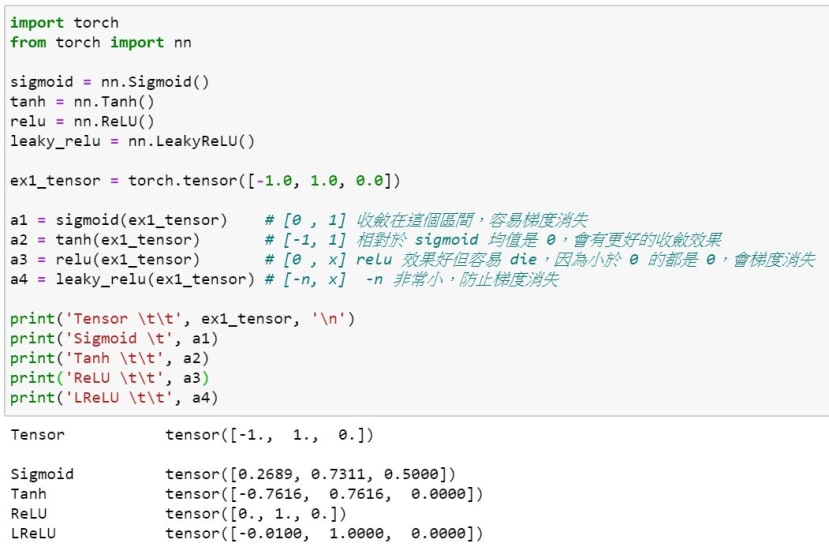
Pytorch使用激励函数一样在torch.nn中呼叫即可，程序代码如下图可以再对照上面的图做确认，像是原本的数值是[ -1. , 1. , 0. ]，经过 Sigmoid函数就变成了 [ 0.26 , 0.73 , 0.5 ] ，因为Sigmoid会将数值 ( x ) 缩限在 [ -1 , 1 ] 之间，最初我在理解激励函数就是直观的认为目标是要将输出缩限到对应的需求，之后才去理解线性与非线性、运算量的问题。

建置一个神经网络

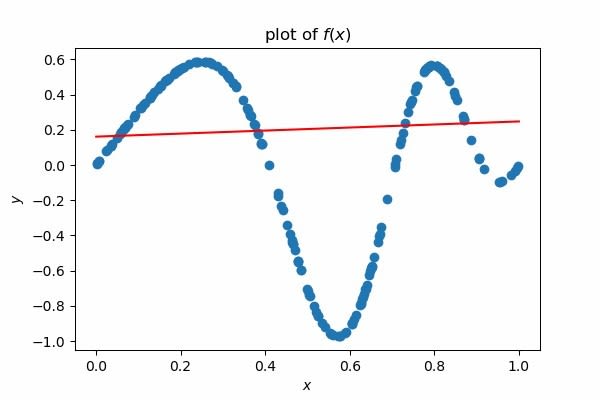
我们先创造一个稍微复杂一点的数据，然后尝试建置一个没有激励函数的神经网络模型并迭代6000次看看效果，接着建置含有激励函数的神经网络模型再比较一次。

建置多层的神经网络其实非常简单，我们一样使用nn.Module来建置，主要的差别在于__init__的部分需多宣告几层，而forward的部分需要将其连接在一起；这边我将激励函数写成方便改变的方式，并且将是否使用激励函数、使用哪个激励函数写在一起，而我的范例提供ReLU、Tanh两种训练结果：

训练的程序代码如下：

第一次训练的时候，我不使用激励函数来训练神经网络，也就是说现在的神经网络只能解决线性的问题，可以从下图观察到该模型没办法收敛到正确答案：

接着我使用ReLU、Tanh来尝试，你会发现在曲线的地方有成功的收敛了，你们可以利用前面提供的激励函数图表来尝试猜猜看哪一个ReLU？

答案是左边是ReLU，你可以注意到没有y值是负的，原因就是ReLU会将输出其收敛在 [ 0 , n ] 之间 ( n表示任意数 )，所以在我们这个案例中使用 ReLU可能就不是个好选择，反观Tanh是将数值收敛在 [ -1, 1 ]　之间，所以在我们的案例中使用它就不会遇到任何问题，由此可知选择激励函数也是一门大学问了，如果你的输出要收敛到哪里就该选择哪个又或者是多个选项输出的话就该选择maxout、输出对与错就使用sigmoid等等。

结语

看完了这篇你已经学会线性回归 ( linear regression) 与逻辑斯回归 (logistic regression)，利用PyTorch建置神经网络的基础也已经都摸透了，下一篇将稍微进阶一些来玩卷积神经网络并做一个小项目。

Pytorch深度学习框架X NVIDIA JetsonNano应用-猫狗分类器