Einführung in die digitale Signalverarbeitung, Teil 3: DACs und Rekonstruktion

Im vorhergehenden Artikel aus dieser Serie, Einführung in die digitale Signalverarbeitung: Abtastung und Aliasing, ging es um die Umwandlung eines kontinuierlichen analogen Signals in eine Reihe digitaler Werte. Dieses Mal betrachten wir den umgekehrten Vorgang.

Mit einem eingebauten Digitalfilter kann der Benutzer einer Kamera für jeden der drei horizontalen Streifen im Bild andere Werte zur Belichtungskorrektur festlegen.
Bildnachweis: Sony

Noch einmal zur Wiederholung: Der Analog-Digital-Wandler (Analogue to Digital Converter, ADC) hat das eingehende Signal mit einer Rate abgetastet, die mehr als doppelt so hoch wie die maximale Frequenzkomponente in diesem Signal ist. Die in digitale Zahlen konvertierten Abtastwerte werden von einem Computer verarbeitet, auf dem ein Algorithmus mit bestimmten Funktionen wie z. B. einem Tiefpassfilter läuft. Die Serie von Abtastwerten, die dieser Algorithmus ausgibt, muss jetzt wieder in eine analoge Signalform gebracht werden.

Der Digital-Analog-Wandler (Digital to Analogue Converter, DAC)

Einfache DACs sind wesentlich unkomplizierter als ADCs. Mit nur wenigen Widerständen und einem Operationsverstärker können Sie selbst einen bauen! Obwohl die meisten Mikrocontroller voll von ADC-Kanälen sind, bieten sie seltsamerweise oft nur wenig Möglichkeiten für eine Umwandlung von digital zu analog. Wie gesagt könnten Sie zwar selbst einen bauen, es empfiehlt sich jedoch, einen fertigen DAC-Chip zu verwenden. Allzweck-DACs sind nicht besonders teuer, und wenn Sie keine außergewöhnlich hohe Geschwindigkeit (Abtastrate) und hohe Auflösung (Bitanzahl) benötigen, können Sie davon ausgehen, dass Monotonizität (der Ausgabewert steigt immer mit jedem zunehmenden digitalen Eingabeschritt) und Linearität (inkrementelle digitale Eingabeschritte erzeugen gleiche Schritte für den Wert der Ausgangsspannung) gegeben sind.

Kriterien bei der DAC-Auswahl

Die Auflösung und der Dynamikbereich des Ausgangssignals beruhen, ebenso wie bei einem ADC, auf der Anzahl der digitalen Bits. In den meisten Fällen ist die DAC-Auflösung mit der des verwendeten ADC identisch. Jedenfalls gibt es keinen Grund, warum der DAC eine höhere Auflösung haben sollte.

Die Abtastrate sollte ebenfalls mit derjenigen des ADC übereinstimmen, aber in vielen Fällen werden Sie feststellen, dass das Datenblatt die Geschwindigkeitskapazität des DAC als Einstellzeit angibt. Hierbei handelt es sich um die Zeit, die vergeht, bis der analog ausgegebene Wert sich innerhalb von ½ LSB des Endwertes einpegelt, wenn der Eingabewert in einem Schritt zwischen Minimal- und Maximalwert wechselt. Bei Verwendung eines DAC mit 8 Bit ist das beispielsweise die Zeit bis zur vollständigen Stabilisierung des Ausgabewerts, nachdem der digitale Eingabewert von 00 auf FFh geändert wurde (ungünstigster Fall). Für diese Einstellzeit gibt es folgende Gründe:

• • Die digitalen Eingabewerte ändern sich nicht gleichzeitig, so dass der DAC für einen kurzen Zeitraum eine ganze Reihe von Eingangscodes „erkennt“.
  • Der Ausgangsverstärker hat eine begrenzte Anstiegsgeschwindigkeit und es dauert nach der Stabilisierung des Eingangswerts einige Zeit, bis der Ausgang den richtigen Wert annimmt.
  • Die Streukapazität kann dazu führen, dass der Ausgangswert zu hoch steigt und „klingelt“.

Während der Einstellzeit wird bei jedem Spannungsschritt des ungefilterten Ausgangswerts ein „Störimpuls“ oder „Klingeln“ angezeigt. Dies ist jedoch in der Regel kein Problem, wenn es nicht länger als ca. 10 % der Abtastzeit dauert. Der Tiefpass-Rekonstruktionsfilter schafft hier Abhilfe.

Der ideale DAC

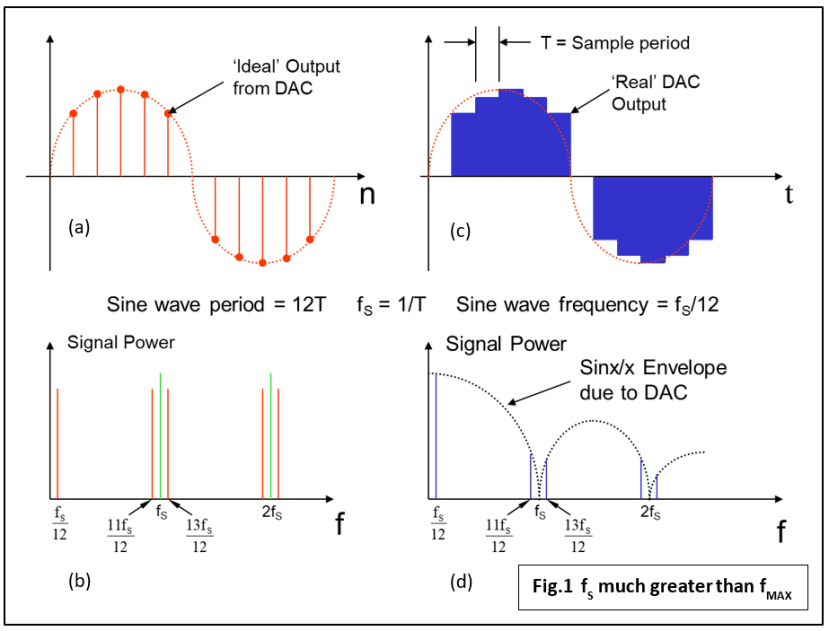
Erinnern Sie sich noch an den „idealen ADC“ vom letzten Beitrag? Theoretisch war sein Abtastintervall Null und daher konnte er eine unbegrenzte Abtastrate haben, ohne dass ein Anti-Aliasing-Filter nötig wurde. Leider haben Bauteile in der Realität eine begrenzte Konvertierungszeit und daher sind auch die Abtastrate und die abtastbare Signalbandbreite begrenzt. Abb. 1a und Abb. 1b zeigen die ideale Ausgabe eines DAC für die Zeit- und Frequenzdomäne. Das digitalisierte Signal ist eine einzelne Sinuswelle. Beachten Sie, dass die gleichen Frequenzkomponenten wie bei den ursprünglich abgetasteten Eingabewerten ausgegeben werden. Das Problem besteht darin, dass kein echter DAC Impulse mit Nullbreite bereitstellen kann und Impulse mit einer endlichen Breite das Signal verzerren.

Echte DACs und die Sinx/x-Verzerrung

Abb. 1c und Abb. 1d zeigen die tatsächliche Ausgabe eines typischen DAC und die daraus resultierende Frequenzverzerrung. Wie Sie sehen, bleibt der ausgegebene Abtastwert während des gesamten Abtastintervalls T konstant. Der Grund dafür ist die Umsetzung mit sehr einfacher Hardware: Ein DAC mit Paralleleingang, der mit verriegelten GPIO-Pins auf einem Mikrocontroller/DSP-Gerät verbunden ist. Die blaue Signalform sieht sehr „blockartig“ aus, kann aber relativ problemlos mit einem analogen Tiefpass- oder „Rekonstruktions“-Filter bereinigt werden, da die Abtastrate zwölf Mal so hoch wie die Signalfrequenz ist. Die im ungefilterten Signal vorhandenen Frequenzkomponenten werden in Abb. 1d dargestellt. Da die ausgegebenen Abtastwerte die gleiche Breite wie das Abtastintervall T haben, werden die Frequenzkomponenten durch eine Sinx/x-Funktion (ausgesprochen „Sinus x über x“) abgeschwächt, wobei die Abtastfrequenz und ihre Oberschwingungen allesamt verschwinden. Die hohe Abtastrate führt dazu, dass die einzige in der Endausgabe (f_S/12), der ursprünglichen Sinuswelle, gewünschte Frequenzkomponente kaum angetastet wird. Der gesamte Rest wird ohnehin vom Rekonstruktionsfilter entfernt.

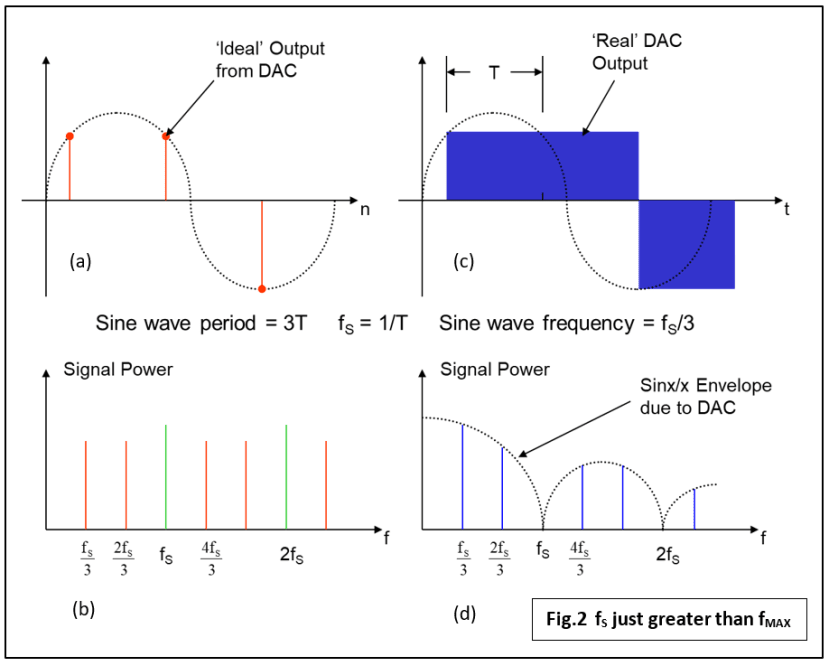
Der Vollständigkeit halber sehen wir uns die gleichen Diagramme für ein Sinuswellensignal mit der Frequenz f_S/3 an, also nur knapp unterhalb der Nyquist-Grenze von f_S/2 (Abb. 2). Der DAC-Ausgang ist sogar noch „blockartiger“, aber das Originalsignal kann dennoch wiederhergestellt werden, da kein Aliasing stattgefunden hat. In Abb. 2d sehen Sie, dass die vorgegebene Sinx/x-Hüllkurve unsere gewünschte Frequenzkomponente f_S/3 eher mehr als zuvor abgeschwächt hat und die nächste unerwünschte Frequenz 2f_S/3 wesentlich näher und größer ist. Stellen Sie sich jetzt vor, dass f_S/3 nur die höchste Komponente in einem Basisband mit Frequenzen ist. Sie sehen, wie die Sinx/x-Verzerrung zu einer deutlichen „Abrollkurve“ über dem Basisband führt.

Rekonstruktion

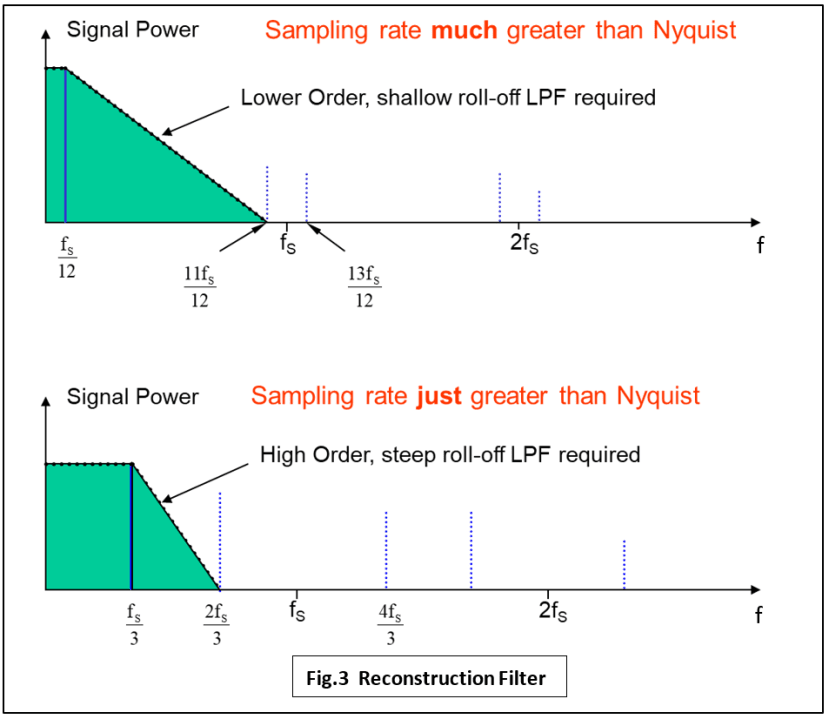
Sowohl Anti-Aliasing- als auch Rekonstruktionsfilter haben das Format eines Tiefpassfilters und übernehmen ähnliche Aufgaben bei der Beseitigung unerwünschter Hochfrequenzkomponenten. Anti-Aliasing-Filter begrenzen die Bandbreite des für den Abtastvorgang bereiten Basisbandsignals, während Rekonstruktionsfilter unerwünschte Frequenzen eliminieren, die sich aus dem Abtastvorgang selbst ergeben (Abb. 3). Daher überrascht es nicht, dass bei der Entwicklung in beiden Fällen ähnliche Überlegungen anzustellen sind: Eine niedrige Abtastrate erfordert einen komplexeren und schnelleren Roll-off-Filter. Eine hohe Abtastrate gestattet die Verwendung einer einfacheren und langsameren Roll-off-Konstruktion.

Digitale Signalverarbeitung

Wir haben nun die Möglichkeit, ein analoges Signal in eine Reihe von Zahlen zu konvertieren, die anschließend wieder in genau dieselbe Signalform umgewandelt werden können. Das ist nicht so sinnlos, wie es klingt, da sich darauf ein Kommunikationssystem zum Versenden analoger Daten über ein digitales Netzwerk aufbauen lässt. Eigentlich geht es aber nicht um Kommunikation: Wir wollen das Signal in seiner digitalisierten Form verarbeiten. Von der einfachen Filterung über die Spektralanalyse bis hin zur Merkmalserkennung in Videobildern ist so ziemlich alles möglich – in Echtzeit. Im nächsten Teil dieser Serie beginne ich mit ein paar einfachen Verarbeitungsalgorithmen. Freuen Sie sich jedoch nicht zu früh: Im Echtzeitbetrieb darf ein Prozesszyklus nicht länger als eine Abtastperiode dauern. Dies bedeutet einen weiteren Kompromiss, bei dem die Attraktivität einer hohen Abtastrate gegen die Komplexität des Prozessalgorithmus abgewogen werden muss.