Getting into Digital Signal Processing Part 3: DACs and Reconstruction
Follow articleHow do you feel about this article? Help us to provide better content for you.
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
What do you think of this article?
The previous article in this series, Getting into Digital Signal Processing: Sampling & Aliasing, covered the process of converting a continuous analogue signal into a series of digital samples. This time we’ll look at the reverse process.
An in-camera digital filter allows the user to set different exposure compensation values for each of three horizontal bands across the image. Image credit: Sony
To recap, the analogue to digital converter (ADC) has sampled the incoming signal at a rate more than twice the frequency of the maximum frequency component present in that signal. These samples, converted to digital numbers, are processed by a computer running an algorithm which performs some function such as a low-pass filter. The series of output samples from this algorithm now needs converting back to an analogue waveform.
The Digital to Analogue Converter (DAC)
Basic DACs are a lot simpler than ADCs. In fact, you can make your own with just a handful of resistors and an op amp! Strangely, while most microcontrollers are loaded with ADC channels, many have little provision for digital to analogue conversion. While you could make your own as I’ve just described, a much better idea is to use a ready-made DAC chip. General purpose DACs are not very expensive, and unless you are looking for very high speed (Sampling Rate) and high resolution (Number of Bits), then Monotonicity (output always increases with each increasing digital input step) and Linearity (Incremental digital input steps provide equal output voltage steps) can be assumed.
DAC Selection Criteria
The Resolution and Dynamic Range of the output signal are based on the number of digital bits just like an ADC. For most purposes, the same DAC resolution will be the same as that of the ADC being used. Certainly, there’s no point in the DAC having a higher resolution.
The sampling rate should also match that of the ADC, but very often you will find that a datasheet will express the DAC’s speed capability in terms of its Settling Time. This is the time it takes for the analogue output to settle down to within ½ LSB of its final value when the input is switched between the minimum and maximum values in one step. Using an 8-bit DAC for example, it’s the time taken for the full-scale output to stabilise after the digital input is switched from 00 to FFh (worst case). This settling time exists because:
- The digital inputs do not change simultaneously, so for a brief interval, the DAC ‘sees’ a whole variety of input codes.
- The output amplifier has a finite slew-rate and it takes time, after the input has stabilised, for the output to change to the correct value.
- Stray capacitance can cause the output to overshoot and ‘ring’.
During the settling time, a ‘glitch’ or ‘ringing’ will be seen on each voltage step of the unfiltered output. It’s not usually a problem though as long as it only lasts for about 10% or less of the sampling period. The reconstruction low-pass filter should remove it.
The Perfect DAC
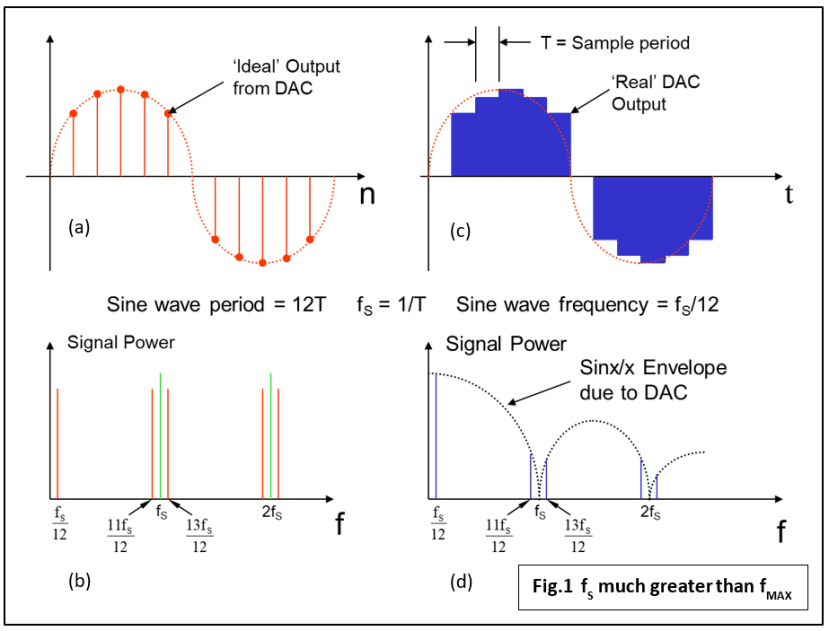
Remember the ‘Perfect ADC’ from last time? In theory, it had a sampling interval of zero and as such could have an infinite sampling rate with no need for an anti-aliasing filter. Unfortunately, practical components have a finite conversion time which means finite sampling rates and a limited signal bandwidth which can be sampled. Fig.1a and Fig.1b illustrate the ideal output from a DAC in the time and frequency domain respectively. The digitised signal is a single sinewave. Note that the output contains the same frequency components as the original sampled input. The problem is that no real DAC can supply zero-width pulses, and finite-width pulses distort the signal.
Real DACs and Sinx/x Distortion
Fig.1c and Fig.1d show the actual output of a typical DAC and the resulting frequency distortion. You can see that an output sample is held constant for the whole sampling interval T. It comes from the simplest hardware realisation: a parallel-input DAC connected to latched GPIO pins on a microcontroller/DSP device. The blue waveform looks very ‘blocky’ but can be cleaned up fairly easily with an analogue low-pass or ‘reconstruction’ filter because the sampling rate is twelve times the signal frequency. The frequency components present in the unfiltered signal are shown in Fig.1d. Because the output samples are the same width as the sampling period T, the frequency components are attenuated by a Sinx/x (pronounced ‘sine x over x’) function, with the sampling frequency and its harmonics disappearing altogether. The high sampling rate means that the only frequency component we actually want in the final output (fS/12), the original sine wave, is barely touched. All the rest would be removed by the reconstruction filter anyway.
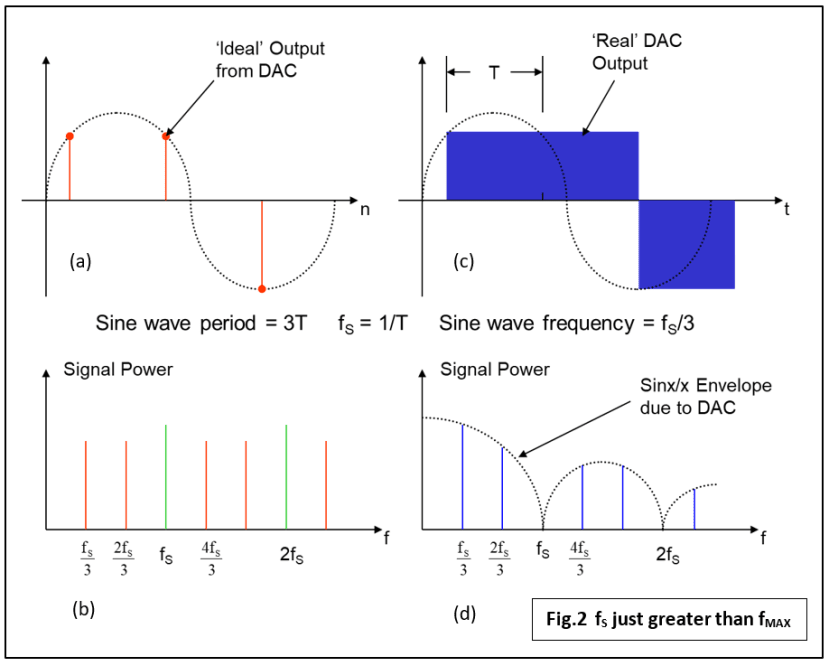
For completeness sake let’s take a look at the same graphs for a sine wave signal of frequency fS/3, only just below the Nyquist limit of fS/2 (Fig.2). The DAC output is even ‘blockier’ but the original signal can still be recovered as no aliasing has taken place. In Fig.2d you can see that the imposed Sinx/x envelope has attenuated our wanted frequency component fS/3 rather more than before and the next unwanted frequency 2fS/3 is much closer and larger. Now imagine that fS/3 is merely the highest component in a baseband of frequencies. See how the Sinx/x distortion introduces a significant curved ‘roll-off’ over the baseband.
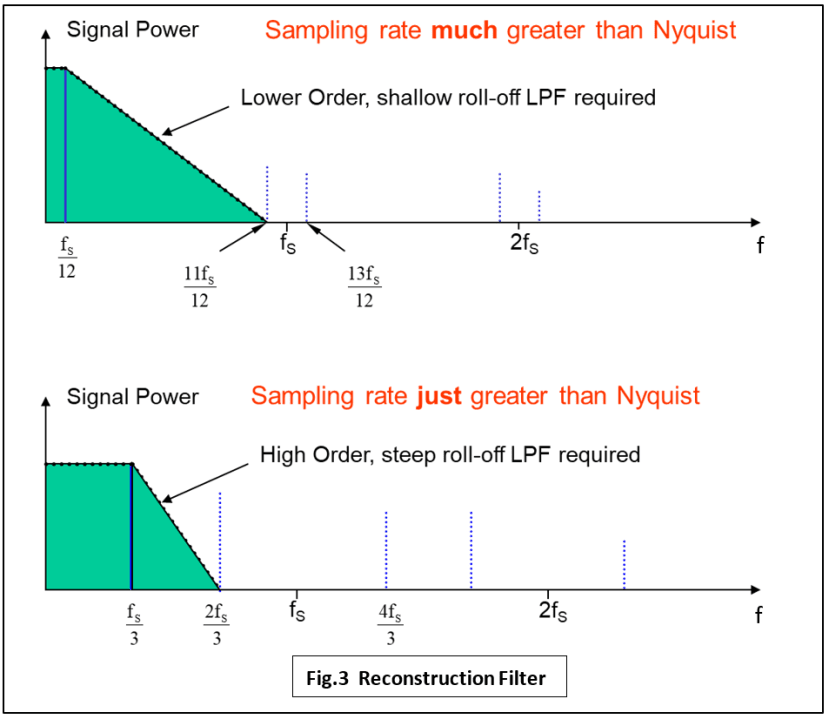
Reconstruction
Anti-aliasing and Reconstruction filters are both low-pass in format and perform similar tasks in removing unwanted high-frequency components. Anti-aliasing band-limits the baseband signal ready for sampling, reconstruction removes the unwanted frequencies resulting from the sampling process itself (Fig.3). No surprise then that design considerations are the same for both: low sampling rate means a more complex and faster roll-off filter. High sampling rate allows a simpler, slower roll-off design to be used.
Digital Signal Processing
So, we now have the means to convert an analogue signal to a series of numbers which can be converted back into precisely the same waveform afterwards. That isn’t as pointless as it sounds because it could form the basis of a communication system for sending analogue data over a digital network. Communication is not the aim here: we want to process the signal in its digitised form. Just about anything is possible from simple filtering, through spectral analysis to feature extraction from video images, all in real-time. I’ll start with some basic processing algorithms in the next part of this series, but before you get excited about all the possibilities, consider this: for real-time operation, a process cycle must take less than one sample period to complete. This means another trade-off, the desirability of a high sampling rate against the complexity of the process algorithm.
Next time in Part 4 we'll look at some popular DSP algorithms.
If you're stuck for something to do, follow my posts on Twitter. I link to interesting articles on new electronics and related technologies, retweeting posts I spot about robots, space exploration and other issues.