Exploring Ethereum with Raspberry Pi Part 2: Creating a Private Blockchain
Follow articleHow do you feel about this article? Help us to provide better content for you.
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
What do you think of this article?
Setting up a brand new test network with preallocated funds and peering nodes.
In part 1 of this series, we explored the basics of Ethereum — which is much more than simply a cryptocurrency and provides a decentralised platform for smart contracts — before proceeding to install the Ethereum geth client, create an account and then run some simple commands.
In this post, we will create a private blockchain and use this to explore Ethereum in a little more detail. Since we’ll be starting with a brand new blockchain we can fully synchronise this and won’t need to configure nodes to use light synch mode.
Stopping mainnet synchronisation
If you followed along with Part 1 and configured a node to use mainnet and run in light synchronisation mode, this can be stopped and start-up disabled with:
$ sudo systemctl stop geth@pi.service
$ sudo systemctl disable geth@pi.serviceCreating a new account
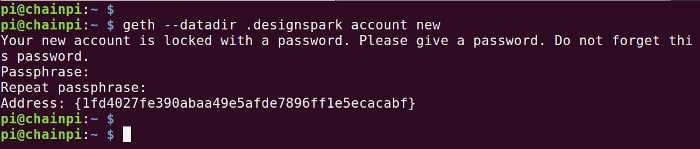
We need a name for our new blockchain network and for the purposes of this example, we’ll use “DesignSpark”. By default Ethereum stores data in a sub-directory of your home directory named “.ethereum”, i.e. a hidden directory on Linux/BSD. So as to keep the data for our private blockchain separate, we’ll use “.designspark”.
If we start by creating a new account:
$ geth --datadir .designspark account newAnd take a note of the address of the account, since we’ll need this when we initialise the new network if we would like to preallocate any funds to it.
In the beginning, there was block 0
There has to be a first link in a chain and a blockchain is no different, requiring a genesis block to be created that will be used by the initial set of nodes which are to participate in the network. This is configured via a JSON file and the contents of the one we used, for example, are below.
{
"config": {
"chainId": 555,
"homesteadBlock": 0,
"eip155Block": 0,
"eip158Block": 0
},
"difficulty": "20",
"gasLimit": "2100000",
"alloc": {
"1fd4027fe390abaa49e5afde7896ff1e5ecacabf":
{ "balance": "20000000000000000000" }
}
}The 'chainId' is a numerical value that identifies the network and a list of those currently in use by public networks can be found here. We needed to pick a number for our private DesignSpark network and for some reason 555 seemed like a good choice — you could use a different number.
So what are the other parameters?
- homesteadBlock. Homestead is an Ethereum release and for our chain, this is set to 0.
- eip155Block. Our chain won’t hard-fork for EIP155, so this is set to 0.
- eip158Block. Our chain won’t hard-fork for EIP158, so this is set to 0.
- difficulty. This sets the mining difficulty and in our case, we want this reasonably low.
- GasLimit. This is the limit of the Gas cost per block.
- alloc. This is where we can pre-allocate funds to accounts.
Ethereum Improvement Proposals (EIPs) describe standards for the Ethereum platform and new ones may be issued to address shortcomings. As a network grows it may be forked at a certain point to allow EIPs to be incorporated. This is not so much a concern for our private network, but for details of where EIP155 was implemented with mainnet and what this does, see Spurious Dragon.
Gas is the unit used as a measure of how much work an action or set of actions takes to perform. Thereby allowing a cost to be attached to executing smart contracts — the objects which contain code functions and that live on the blockchain and are able to interact with other contracts, make decisions, store data, and send ether to others. More on this in a future post.
Alloc allows us to preallocate funds to one or more accounts. Here funds have been allocated to the address of the account we created earlier.
Having saved our config file to designspark.json we can now initialise the network with:
$ geth --datadir .designspark init designspark.jsonAnd that’s it, we’ve written out our genesis block and now have the very beginnings of our new network. Provided subsequent nodes are initialised in the same way, they can become members too.
Starting the first node
To start the first node with the JavaScript console we enter:
$ geth --identity chainpi --rpc --rpcport 8080 --rpccorsdomain "*" --datadir .designspark --port 30303 --nodiscover --rpcapi "db,eth,net,web3" --networkid 555 consoleWhat do all the parameters mean?
- indentity. This sets the Ethereum node identity.
- rpc*. The various RPC settings configure the available APIs and who has access to them.
- datadir. We obviously need to use the same data directory as before.
- nodiscover. This means our node is not discoverable.
- networkid. This needs to be the same numerical ID configured during initialisation.
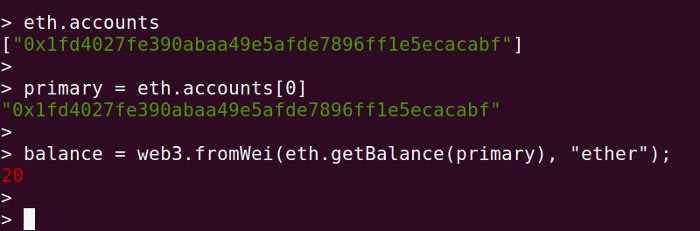
Once we’ve entered the console we can use eth.accounts to list the available accounts and eth.getBalance to check the balance.
> eth.accounts
> primary = eth.accounts[0]
> balance = web3.fromWei(eth.getBalance(primary), “ether”);Note how the figure returned is much smaller than what we preallocated via designspark.json? That’s because the balance in Ether was returned, whereas during initialisation the allocation was actually specified in Wei, a far smaller unit.
Creating a 2nd node
A blockchain network with only one node wouldn’t be much use and so we’ll create a second one. This time it’s recommended to use a computer with a little more RAM, such as a laptop or desktop running Debian/Ubuntu, as this is likely to be needed should we wish to run a miner at some point.
To recap, the steps involved are:
- Install geth.
- Run the command as above to create a new account.
- Initialise using the same JSON configuration file.
- Start the node as before, but this time use a different identity!
Once we’ve done this, the node has been started and dropped into the JavaScript console, we can then once again check the new account and its balance with:
> eth.accounts
> primary = eth.accounts[0]
> balance = web3.fromWei(eth.getBalance(primary), “ether”);This time we should see we have a balance of 0, as we didn’t preallocate any funds to the account.
Connecting the peers
Since we don’t want our nodes to be discoverable we started them with the --nodiscover option, meaning that we’ll need some way of configuring them to peer. We can achieve this by creating a file called static-nodes.json located in the datadir, which in our case is ~/.designspark.
First, though we need to get the enode URL for each of our nodes by entering at the JavaScript console on each system:
> admin.nodeInfo.enodeWe then populate the static-nodes.json file with this info as follows:
[
"enode://01f5ecc7c232f7571175bffc71c4e1608e1308e2ce7fd6ed3ae17d5e97e2d5253dcaa854286f99991d671788127f7902fa56d20875eabae49665a515da105047@10.100.1.196:30303", "enode://5156218119a3697389a34bf0a19ceca49d9f3d06948836b8cc6c206c9f7b7081e64537eeb0f9c059561736a8e7cb6ebbe438028dd949d0f69f4cab642c11d46c@10.100.1.229:30303"
]Note how [::] has been replaced by the node IP address and the ?discport=0 suffix omitted.
Once this file has been created on both nodes we can exit geth via CTRL-D and then re-launch the console. Following which if we enter on the first node:
> admin.peersWe should see the details for the second node.
Repeating this on the second node we should then see the node info for the first.
So now we have our own private blockchain network complete with two nodes, each configured with an account and one of those with preallocated funds.
In part 3 of this series we will move on to transacting with the network — transferring funds, executing a smart contract and mining Ether.