Blockchain Primer – Part 3
Follow articleHow do you feel about this article? Help us to provide better content for you.
Thank you! Your feedback has been received.
There was a problem submitting your feedback, please try again later.
What do you think of this article?
In part 2 of our primer, we discussed the idea that a decentralised peer-to-peer system like a public blockchain, needs to achieve consensus on both the chain history and what new data is allowed to be added, in order to be effective. Of course, that is easier said than done, especially when thousands of nodes are in play.
The seminal paper exploring this problem is a thought experiment published in 1982 by Leslie Lamport, Robert Shostak and Marshall Pease called The Byzantine Generals Problem. As academic papers go, it’s an easy read and well worth your time.
The Byzantine Generals Problem
As a way of conceiving a situation where several parties need to create a consensus about their future actions, despite the possible existence of rogue or traitorous elements within the group, the paper describes a scenario where several generals of the old Eastern Roman Empire are positioned around a rebellious city. Each general and their army is in a separate camp and communication between camps is only possible by messenger over open (possibly hostile) terrain.
The problem for the generals is the strength of the city they are besieging. The city can easily crush a single army and can withstand an uncoordinated attack from multiple armies. For the generals to succeed, they must attack in unison. The other option, that will allow them to maintain the strength to fight another day, is to decide to retreat together.
In terms of the messaging that each general must send to create this outcome, the paper shows that the problem for each individual general (in its simplest form) looks like one that can be described by a commanding general and two lieutenants. The conditions laid out in the paper are:
Byzantine Generals Problem. A commanding general must send an order to his n-1 lieutenant generals such that
IC1. All loyal lieutenants obey the same order.
IC2. If the commanding general is loyal, then every loyal lieutenant obeys the order he sends.
Seems simple enough, but when our generals use open (or oral) messages, there is no solution unless more than 2/3 of the generals are loyal. Put the other way, for our 3 generals, no solution will work in the presence of a single traitor. This can be illustrated in the following two figures:
In Fig 1, the Commander orders both lieutenants to attack. Lieutenant 2 is a traitor and messages Lieutenant 1 that he received a retreat order. To satisfy condition IC2, Lieutenant 1 will obey the order to attack.
However, in Fig 2 where the Commander is the traitor, he sends an attack order to Lieutenant 1 and a retreat order to Lieutenant 2. Not knowing who the traitor is, or what message was sent to Lieutenant 2, Lieutenant 1 finds himself with exactly the same information as he received in Fig 1. As long as the traitor is consistent in their lies, Lieutenant 1 will always have to attack.
The paper goes on to show mathematically that no solution with fewer than 3m + 1 generals can cope with m number of traitors: i.e. fewer than 1/3 of the generals can be a traitor for there to still be a viable solution.
Stop The Fake News
As we saw in Fig 1 and Fig 2, the ability of the traitor(s) to lie is what makes the Byzantine Generals Problem so pithy. We can make the solution easier if we can restrict the ability to lie. This can be done by sending messages with signatures that cannot be counterfeited. The assumptions that are made in this case are:
A1. Every message sent is delivered correctly
A2. The receiver of the message knows who sent it
A3. The absence of a message can be detected
These assumptions were also true for the previous ‘oral message’ examples, but what we add at this point is:
A4. (a) A loyal general’s signature cannot be forged and any alteration of the contents of his signed messages can be detected.
(b) Anyone can verify the authenticity of a general’s signature.
In this scenario, the commander sends a signed order to each of his lieutenants. Each Lieutenant will then add their own signature to the order before sending it to the other lieutenant(s) and so on. If we apply this algorithm to the previous scenario we get this:
The Commander signs his orders with ‘0’. Each Lieutenant signs the order he received and sends it on to the other. In this case, the lieutenants know their commander is a traitor as his signature is on two opposing orders and A4 states only he could have generated the signature.
The paper goes on to show mathematical proofs for the fact that this algorithm can now cope with m traitors for any number of generals and for how this works in other scenarios such as when there are missing communication paths. That is probably outside the scope of a ‘primer’ article and if you have read the earlier parts of this article, I think you will already see how these ideas are employed (using cryptography to create signatures) as the basis of how blockchains reach consensus and resist attack.
Orphans, Uncles and Going Stale
Remember that each miner across a blockchain network is trying to be the first to solve the cryptographic puzzle for the current block? Once it is solved, the miner sends the solution to the network for verification. Assuming all is OK, the miners will then start on the next block.
But what happens if two miners solve the same block at the same time? All distributed networks have latency, as it takes time for the data to ripple through to all nodes. This could be anything from a few milliseconds to a few seconds which means it is quite possible that two separate miners will have had their blocks validated and added to the chain by a large number of nodes.
We now have a fork in our blockchain which will grow as two separate chains, as they are both valid and mining cannot stop while this gets sorted out. This is a problem for a blockchain as, just like in Highlander, there can be only one.
Different blockchains have their own approaches to solving this dilemma so we will look at how the most common, Bitcoin and Ethereum, get back on an even keel.
Bitcoin
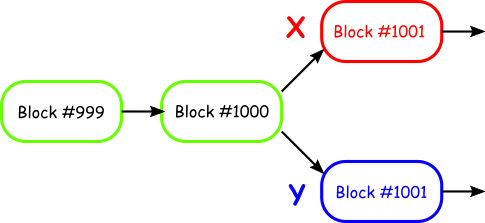
Let’s consider a situation where miner X and miner Y have both just solved block number 1001. Due to being in a part of the world with lower network latencies, miner X has passed on his new block to 60% of the Bitcoin network. Miner Y has passed his block to the other 40%. At this point in time, both blocks are considered valid and mining continues.
The mining nodes that accepted miner X’s block are mining to add the next block after miner X’s block, whereas the nodes that accepted miner Y’s block will be mining to add to Y’s chain.
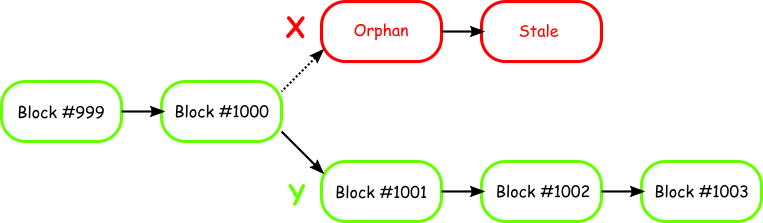
The miners adding to X’s chain add another block but the miners adding to Y’s chain have added two blocks. In a blockchain, chain length is king so, despite having more nodes mining X’s chain, it will be Y’s longer chain that takes the spoils and is accepted as the true chain.
X’s block #1001 gets cut off from the chain and remains without a parent block so is now referred to as an orphan block. X’s miners will get no reward for the extra block they found, which is now an unusable stale block.
In a real implementation, the blockchain network will not wait so long to make the decision. As soon as block #1002 is mined, the network will switch to that chain and orphan the other.
In case you were wondering what happens to the transactions that made up the orphaned (and stale) block: they automatically go back into the queue to be added to the next block.
Ethereum
Ethereum has a slightly different approach to this question in the form of the GHOST (Greedy Heaviest Observed Subtree) protocol, which rewards miners that find what would be orphan and stale blocks in Bitcoin. In Ethereum, they are called Uncle blocks and while they are still not added to the main blockchain, a miner gets a reward, albeit lower than for a standard block that is added to the chain.
Ethereum allows 7 levels of Uncle blocks – equivalent to an orphan block and six stale blocks in Bitcoin – and rewards them according to a formula:
([Uncle block number] + 8 – [Block number]) x ([Ethereum reward] /8)
So if the reward for a standard block was 3ETH, then the first Uncle block would be worth 2.625ETH, the next would be 2.25ETH followed by 1.87ETH and so on. Again, in a real implementation, a miner node will abandon the Uncle chain after one (or at most, two) blocks.
Going Forward
Blockchain is a developing technology and I expect that the most beneficial uses for the technology will come quite some time after the mainstream hype has died down. They will probably also require some fundamental advances in the underlying technology to make it truly useful.
As an example of what I mean, Martin Cooper was working for Motorola in 1973 when he filed a patent for a ‘Radio Telephone System’. He made the first mobile phone call the same year, but it wasn’t until the rollout of the digital GSM networks in the mid 1990s (which in turn allowed for lower power, cheaper handsets and broader cell coverage through much more efficient use of transmission bandwidth than was possible with analogue technology) that the technology could start to become ubiquitous and add previously unthought-of features.
Similarly, blockchain has some limitations it needs to overcome. For example, the Bitcoin blockchain can only process 7 transactions per second and mining a block takes an average of 10 minutes. This curbs its usefulness to financial institutions that handle millions of transactions per day. That is without considering the fact that each individual transaction added to a block effectively requires the same energy as 1.6 average US households would use in 24 hours. Then there is the size of the chain which, at over 25GB and growing, is getting harder and harder to fit onto personal devices.
On the flip side, there is a lot of money going into research with groups like the Global Blockchain Business Council (GBBC) actively seeking to develop new uses for blockchain and the Hyperledger Project working to create open standards to allow for cross-industry interoperability. IBM in partnership with Samsung has been working on ADEPT (Autonomous Decentralized Peer-to-Peer Telemetry) using blockchain tech to secure distributed networks of autonomous devices in a decentralized IoT ecosystem.
At the present time, blockchain can find applications for the kinds of data that would have been traditionally kept in a ledger such as financial transactions (including microtransactions), local government records (voting, land and vehicle registration etc.), medical data, tracking data and similar. However, I can foresee improvements in the underlying technology allowing many other kinds of secure data storage applications to become viable.